Enunciado
Ciência dos Materiais - Callister - Ciência e Engenharia de Materiais. Uma Introdução- Ed: 8º - Capítulo 8.Perguntas e Problemas - Ex. 15
Uma barra cilíndrica em aço 1045 (Figura 8.34) é submetida a um ciclo repetido de tensões de tração e de compressão ao longo do seu eixo. Se a amplitude da carga é de 22000N (4950 ), calcule o diâmetro mínimo admissível da barra para assegurar que não ocorrerá falha por fadiga. Assuma um fator de segurança de 2,0.
Passo 1
A figura 8.34 está abaixo:
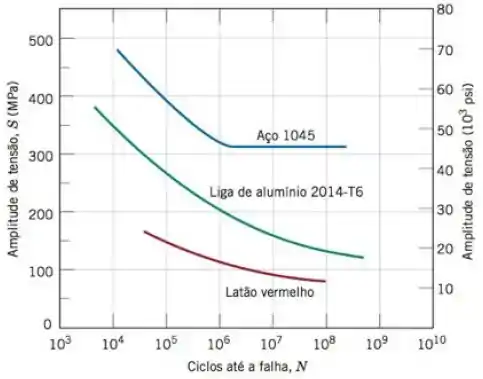
Na Figura 8.34, a amplitude de tensão do limite de fadiga para esta liga é de 310 MPa (45.000 psi). A tração é definida na Equação 6.1 como . Para uma barra cilíndrica:
A substituição de na Equação 6.1 leva a:
Passo 2
Agora resolvemos o , considerando o estresse o limite de fadiga dividido pelo fator de segurança.
Portanto:
Resposta
Exercícios de Livros Relacionados
Um ensaio de fadiga foi conduzido tal que a tensão média era de 50MPa (7250psi) e a amplitude de tensão era de 225MPa (32625psi).Calcule os níveis de tensão máximo e mínimo.Calcule a razão entre as te
Cite cinco fatores que podem levar à dispersão em dados da vida em fadiga.
Três corpos de provas de fadiga idênticos (identificados como A , B e C ) são fabricados a partir de uma liga não ferrosa. Cada um é submetido a um dos ciclos de tensão máxima – mínima listados na tab
Os dados de fadiga para um ferro fundido nodular estão dados a seguir:Trace um gráfico S - N (amplitude da tensão em função do logaritmo do número de ciclos até a falha) usando esses dados.Qual é o li
Suponha que os dados de fadiga para o ferro fundido no Problema 8.20 tenham sido obtidos a partir de ensaios giratórios com dobramento e que uma barra dessa liga deva ser utilizada em um eixo de autom