Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Ciência dos Materiais - Callister - Ciência e Engenharia de Materiais. Uma Introdução- Ed: 8º - Capítulo 7.Problemas de Projetos - Ex. P5

Uma barra cilíndrica de aço 1040, originalmente com 15,2   m m   0,60   i n de diâmetro, deve ser trabalhada a frio por estiramento. A seção transversal circular será mantida durante a deformação. Um limite de resistências à tração superior a 840   M P a   122000   p s i e uma ductilidade de pelo menos 12   %   A L são desejados após o trabalho a frio. Adicionalmente, o diâmetro final deve ser de 10 m m   0,40   i n . Explique como isso pode ser conseguido.

Passo 1

Esse problema nos leva a explicar o procedimento pelo qual uma haste cilíndrica de aço 1040 pode ser deformada para produzir um determinado diâmetro final ( 10   m m ) , bem como uma resistência à tração mínima específica ( 8 40   M P a ) e ductilidade mínima ( 12 %   A L ) . Primeiro, vamos calcular a porcentagem de trabalho a frio e a resistência à tração e ductilidade se o nosso processo for realizado sem interrupção. Da equação 7.8 temos que

% T F = A 0 - A d A 0 × 100 = π r 0 2 - π r d 2 π r 0 2 × 100

% T F = π ⋅ d 0 2 2 - π ⋅ d 2 2 π ⋅ d 0 2 2 × 100       i

% T F = 1 - d d 0 2 = 1 - 10 15,2 2 ≈   56,7 % T F

Para 56,7 %   T F , nosso aço terá uma resistência à tração da ordem de 900   M P a (Figura 7.19(b)), o que é adequado, no entanto, a ductilidade será menos que 9 %   A L (Figura 7.19(c)), o que é insuficiente.

Passo 2

Agora, em vez de executar essa operação em uma única operação, vamos inicialmente fazer uma porção de deformação total, depois recozir para recristalizar e, finalmente, trabalhar a frio o material uma segunda vez para alcançar o diâmetro final, a resistência à tração e ductilidade. Observando a Figura 7.19   ( b ) dada por

Nos indica que são necessários cerca de 19 % de trabalho a frio para produzir uma resistência à tração de 8 40   M P a . Da mesma forma, pela figura 7.19   c temos que é possível um valor máximo de 19 % de trabalho a frio para que tenhamos 12 %   A L como pode ser comprovado através da figura 7.19 c

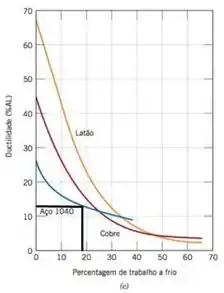
Isso indica que estamos em um bom caminho. Pois bem, se o diâmetro final após o primeiro processo for   d 0 ' , então usando nosso valor de 19 %   T F na equação i   teremos

% T F = 1 - d d 0 2 → d 2 d 0 ' 2 = 1 - % T F →   d 0 ' = d 1 - T F 100

d 0 ' = 10 1 - 19 100 ≈ 11.11   m m  

Ou seja, devemos ter um diâmetro inicial dado com o valor acima para que possamos conseguir efetuar tudo como descrito no enunciado.

Resposta

Devemos ter um diâmetro inicial dado com o valor acima para que possamos conseguir efetuar tudo como descrito no enunciado.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma barra cilíndrica de latão, originalmente com 16,0mm (0,625in) de diâmetro, deve ser trabalhada a frio por estiramento. A seção transversal circular será mantida durante a deformação. Um limite de
Um corpo de provas cilíndrico de aço trabalhado a frio possui uma dureza Brinell de 250 . a Estime sua ductilidade em termos dos alongamentos percentual. b Se o corpo de provas permaneceu cilíndrico d
Determine se é possível trabalhar a frio um aço para obter uma dureza Brinell mínima de 225 e, ao mesmo tempo, ter uma ductilidade de pelo menos 12 % A L . Justifique sua decisão.
Determine se é possível trabalhar a frio o latão para obter uma dureza Brinell mínima de 120 e, ao mesmo tempo, ter uma ductilidade de pelo menos 20% A L . Justifique sua decisão.