Uma bobina com 0,1 m de comprimento com 15 espiras conduz uma corrente de 1,0 A.

1. Calcule a densidade do fluxo se a bobina está no vácuo.
2. Uma barra de uma liga ferro-silício, para a qual o comportamento B-H está mostrado na Figura 20.29, está posicionada no interior da bobina. Qual é a densidade de fluxo nessa barra?

1. Suponha que uma barra de molibdênio seja agora colocada no interior da bobina. Qual corrente deve ser usada para produzir no Mo o mesmo campo B que foi produzido na liga ferro-silício usando 1,0 A?

Vamos começar calculando a intensidade do campo então:

Agora vamos calcular a densidade do fluxo:

Pra resolver a letra (b), vamos dar uma olhada nessa Figura que ele falou no enunciado:

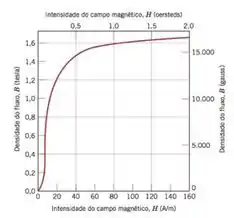
Vemos então no gráfico, que quando

Para resolver essa questão, vamos começar vendo as fórmulas que temos:

Mas o molibdênio, é uma substância paramagnética e podemos pegar seu da tabela 20.2:

Substituindo os valores que já temos:

Com o valor de , podemos usar a mesma fórmula do Passo 1, da intensidade do campo magnético:

Resolvendo para :