Enunciado
Ciência dos Materiais - Callister - Ciência e Engenharia de Materiais. Uma Introdução- Ed: 8º - Capítulo 18.Perguntas e Problemas - Ex. 50
Um capacitor de placas paralelas com dimensões de 100 mm por 25 mm e com uma separação entre as placas de 3 mm deve ter uma capacitância mínima de 38 pF () quando um potencial CA de 500V for aplicado em uma frequência de 1 MHz. Quais dentre os materiais listados na Tabela 18.5 são possíveis candidatos? Por quê?
Passo 1
Pra resolver essa questão vamos usar a fórmula do capacitância:
E a fórmula da constante dielétrica:
O que a gente vai ter que fazer então é primeiro calcular o mínimo pra esse material. E com ele calcular a constante dielétrica mínima. Sabendo esse valor, a gente olha na tabela e vê quais materiais tem constante dielétrica maiores ou iguais, que vão ser aptos pra serem usados nesse capacitor!
Passo 2
Vamos começar calculando a permissividade então:
Passo 3
Agora vamos calcular a constante dielétrica mínima:
Passo 4
Pronto, agora que sabemos a constante dielétrica mínima, vamos lá olhar na tabela quais materiais se encaixam:
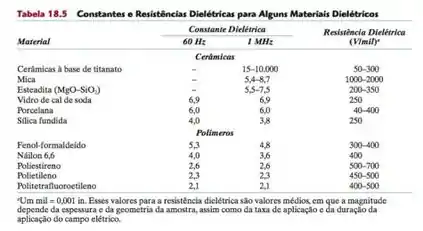
Como a frequência aplicada é 1 MHz, os candidatos possíveis são: Esteadita, Mica e Cerâmicas à base de titanato.
Resposta
Esteadita, Mica e Cerâmicas à base de titanato. Pois esses materiais tem constante dielétrica maior que a mínima necessária para aguentar o potencial aplicado.