Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Ciência dos Materiais - Callister - Ciência e Engenharia de Materiais. Uma Introdução- Ed: 8º - Capítulo 3.Perguntas e Problemas - Ex. 12

Considerando os dados de peso atômico, estrutura cristalina e raio atômico que estão tabulados na parte interna da capa deste livro, calcule as massas específicas teóricas para chumbo, cromo, cobre e cobalto e, então, compare esses valores com as massas específicas medidas que estão listadas na mesma tabela. A razão c/a para o cobalto vale 1,623.

Passo 1

Para calcular a massa específica teórica de um sólido metálico usamos a seguinte fórmula:

ρ = n A V c N A

Onde:

n é o número de átomos associado a cada célula unitária;

A é o peso atômico;

V c é o volume da célula unitária;

N A é o número de Avogrado igual a 6,023   x   10 23 partículas;

Precisamos calcular as massas específicas teóricas do chumbo, cromo, cobre e cobalto que são estruturas cristalinas do tipo CFC, CCC, CFC, HC respectivamente. Então vamos nessa?!

Passo 2

Vamos começar pelo chumbo que tem estrutura cúbica de face centrada (CFC) que nem na figura ai:

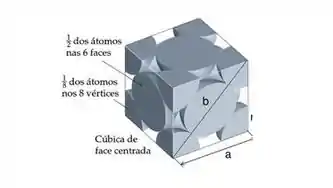
Nesse caso temos n = 4 e V c por sua vez pode ser calculado por:

V c = a 3

Na estrutura CFC, como podemos ver na figura lá em cima, podemos relacionar os raios das esferas com a diagonal da face do cubo. Usando a seguinte relação:

4 r = a 2

Então temos:

a = 2 R 2

Da tabela:

r = 1 , 75 × 10 - 8   c m

Substituindo e calculando:

ρ = n A V c N A

ρ = 4 × 207,2 2 × 1 , 75 × 10 - 8 2 3 × 6,023 × 10 23 = 11,35 g c m 3

Passo 3

Para o Cromo, vamos fazer um procedimento muito parecido, porém como a estrutura dele é cúbica de corpo centrado (CCC), igual da figura abaixo:

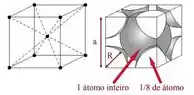
Nesse caso temos dois átomos, então a relação entre a aresta e o raio pode ser escrita da seguinte forma:

4 r = a 3

a = 4 r 3

Da tabela temos que:

r = 1 , 2 5 × 10 - 8   c m

Usando a fórmula da densidade temos:

ρ = 2 × 52,00 4 × 1 , 25 × 10 - 8 / 3   3 × 6,023 × 10 23

ρ = 7,18 g c m 3

Passo 4

Para o cobre fazemos a mesma coisa que fizemos lá no chumbo, afinal ambos são CFC! Então:

ρ = n A 2 r 2 3 N A

Da tabela temos que:

r = 1,28 × 10 - 8   c m

Então:

ρ = 4 × 63,50 2 × 1 , 28 × 10 - 8 2 3 × 6,023 × 10 23 = 8,89 g c m 3

Passo 5

Por último, pra fazer pro cobalto vai ser um pouquinho mais trabalhoso, já que a estrutura é hexagonal. Mas a primeira parte é a mesma coisa, vamos encontrar a massa dentro da célula!

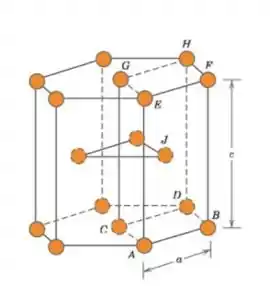
Pro cálculo do volume, precisaremos fazer a área do hexágono vezes a altura c . Olhando só pro hexágono da “tampa” a gente tem a relação: a . Sendo assim

a = 2 r

Do enunciado temos que:

c = 1,623   a

Da tabela:

r = 1 , 2 5 × 10 - 9 c m

Para calcular o volume usamos a fórmula do prisma hexagonal:

V c = 3 a 2 c 3 2

Substituindo as relações acima:

V c = 3 × 1,623   2 R 3 3 2

V c = 3 × 1,623   2 × 1 , 25 × 10 - 8 3 3 2

V c = 6,59 × 10 - 23   c m 3 / u n i d a d e   d e   c e l u l a

Agora finalmente podemos calcular a massa específica:

ρ = 6 × 58,93 6,59 × 10 - 23 × 6,023 × 10 23

ρ C o = 8,91   g / c m ³  

Resposta

ρ P b = 11,35   g / c m ³

ρ C r = 7,18   g / c m ³

ρ C u = 8,893   g / c m 3

ρ C o = 8,91   g / c m ³

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Esboce uma célula unitária para a estrutura cristalina ortorrômbica de corpo centrado.
Esboce uma célula unitária tetragonal e no interior dessa célula indique as localizações dos pontos com coordenadas 1 2 1 1 2 e 1 4 1 2 3 4 .
Empregando o Utilitário Molecule Definition (Definição de Moléculas), encontrado nos módulos “Metallic Crystal Structures and Crystallography” e(Estruturas Cristalinas Metálicas e Cristalografia) e “C
O rênio possui uma estrutura cristalina H C , um raio atômico de 0,137n m e uma razão c / a de 1,615 . Calcule o volume da célula unitária para o R e .
Liste as coordenadas dos pontos para os íons titânio, bário e oxigênio de uma célula unitária da estrutura cristalina da perovskita (Figura 12.6 ).