Enunciado
Ciência dos Materiais - Callister - Ciência e Engenharia de Materiais. Uma Introdução- Ed: 8º - Capítulo 9.Perguntas e Problemas - Ex. 34
Considere o diagrama de fases eutético hipotético para os metais A e B, o qual é semelhante àquele para o sistema chumbo-estanho, Figura 9.8. Assuma que (1) as fases e existem, respectivamente, nas extremidade A e B do diagrama de fases; (2) a composição eutética é de 47%p B-53%p A; e (3) a composição da fase na temperatura eutética é de 92,6%p B-7,4%p A. Determine a composição de uma liga que irá gerar frações mássicas de primária e total de 0,356 e 0,693, respectivamente.
Passo 1
Pra resolver essa questão, a gente vai precisar analisar o diagrama de fases da liga chumbo-estanho, que vamos usar como se fosse A-B.
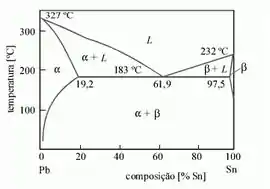
O que ele quer dizer nas hipóteses é:
- A = Chumbo (Pb) e B = Estanho (Sn) no diagrama de fases
- Ali aonde tá esse 61,9, pra nossa liga A-B, vai ser 47%p B (na escala de composição)
- Ali aonde tá 97,5, pra nossa liga A-B, vai ser 92,6%p B.
Beleza, então pra gente resolver a nossa questão, a gente vai ter 2 incógnitas. Qual valor que vai estar no lugar daquele 19,2 e a composição da liga que a questão quer. Pra isso, a gente vai fazer a regra da alavanca duas vezes, uma abaixo e uma acima da linha da temperatura eutética, e isso vai dar pra gente um sisteminha com 2 equações pra gente resolver nossa questão.
Ah, e uma dica que o enunciado dá pra gente é que a liga que ele quer tem que fazer fase primária e eutética, então essa composição vai estar naquela região ali do , entre o valor que a gente não sabe e o 47%p B. Beleza? Bora fazer então!
Passo 2
Como queremos que a composição de primária seja igual a 0,356, a regra da alavanca acima da temperatura eutética tem que ficar assim:
Onde x é a composição da liga e y é a composição eutética de .
Pra composição global, queremos fração de total igual a 0,693. Então nossa regra da alavanca vai ficar com essa cara:
Passo 3
Agora que temos as duas equações do nosso sistema, já conseguimos resolver. Como o problema só quer a composição da liga, a gente vai pegar uma das equações e isolar o y, deixando tudo em função de x, pra depois substituir na outra. Beleza?
Passo 4
A agora é só substituir e achar x!
Lembrando que essa é a composição de B!
Resposta
32,193%p B - 67,807%p A