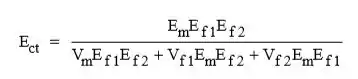Derivar uma expressão generalizada análoga à Equação 16,16 para o módulo transversal de elasticidade de um composto híbrido alinhado constituído de dois tipos de fibras contínuas.
Passo 1
VAMO QUE VAMOOOO! Este problema pede que se obtenha uma expressão generalizada análoga à Equação 16.16 para o módulo transversal de elasticidade de um composto híbrido alinhado constituído de dois tipos de fibras contínuas. Denominemos os subscritos f1 e f2 para os dois tipos de fibras, e m , c, e t para a matriz, composto, e direção transversal, respectivamente. Para o estado de isostress, as expressões análogas às Equações 16.12 e 16.13 são
![]()
E,
![]()
Passo 2
Como , fazendo substituições da forma desta equação na expressão anterior, resulta,
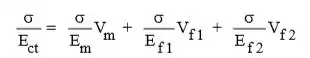
Logo,
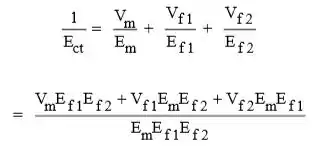
Passo 3
E finalmente, pegando a reciprocidade dessa equação, nos leva a,