Enunciado
Ciência dos Materiais - Callister - Ciência e Engenharia de Materiais. Uma Introdução- Ed: 8º - Capítulo 14.Perguntas e Problemas - Ex. 19
- Determine a razão entre as unidade repetidas de butadieno e estireno em um copolímero que tem uma massa molar numérica média de e um grau de polimerização de 4425.
- Qual(is) será(ão) o(s) tipo(s) desse copolímero, considerando as seguintes possibilidades: aleatório, alternado, enxertado e em bloco? Por quê?
Passo 1
Pra responder essa questão vamos calcular primeiro a massa do copolímero! Como vamos fazer isso? Dividindo a massa molar numérica média do polímero por metade do grau de polimerização (já que estamos falando de 2 unidades). Dai vamos encontrar a massa de 1 mero (unidade que se repete no polímero).
A gente também vai precisar saber a massa de cada uma das estruturas e com isso a gente calcular a fração de cada uma. E ai pronto, temos a resposta da letra a! Com essa resposta a gente analisa a resposta da letra b!
Bom, vamos então começar vendo as massas!
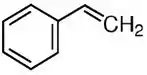
Estireno:
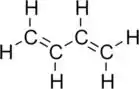
Butadieno:
Pela estrutura podemos ver que a massa do estireno é: .
A massa do butadieno é então: .
Passo 2
Vamos agora então calcular a massa do copolímero:
Passo 3
Pra esse caso a gente consegue ver que a massa que a gente achou do mero é praticamente igual a soma das massas das unidades. Isso indica pra gente que a proporção é então 50%-50%.
Essa proporção é comum para estruturas lineares alternadas, onde uma molécula de uma unidade vem seguida da outra ao longo da cadeira. Maaaaas, o polímero pode ser em aleatório, em blocos ou enxertado, desde que pra cada molécula de um haja uma molécula de outro,
Resposta
- A razão entre as duas unidades é 1:1.
- O mais provável é que seja um polímero alternado, mas qualquer todas as outras opções são possíveis, desde que a proporção da letra a seja mantida.