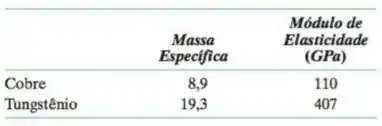
Deve ser preparado um compósito com partículas grandes de tungstênio em uma matriz de cobre. Se as frações volumétricas de tungstênio e cobre são de e , respectivamente, estime o limite superior para a rigidez específica desse compósito a partir dos dados a seguir.

Desejamos estimar o limite superior para a rigidez específica do nosso compósito descrito no enunciado. Pois bem, existe mais de uma forma de fazermos essa estimativa mas como somos alunos sagazes vamos utilizar a forma mais prática não é mesmo? Afinal de contas ninguém quer ter trabalho extra desnecessário. Temos que nossa rigidez específica é dada pelo coeficiente do módulo de elasticidade pela massa específica, ou seja,

Dessa forma, vamos adaptar a equação de forma que possamos, trabalhando com ela, encontrar direto o que precisamos. Assim, vamos escrevê-la da seguinte forma

Pronto, está resolvido nosso problema da forma mais prática.