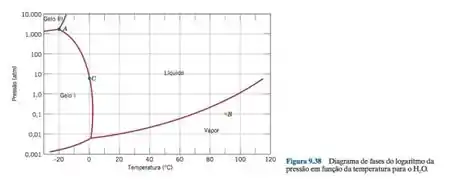
A Figura 9.38 mostra o diagrama de fases pressão-temperatura para o . Aplique a regra das fases de Gibbs para os pontos A, B e C; isto é, especifique o número de graus de liberdade em cada um desses pontos – ou seja, especifique o número de variáveis controláveis externamente que precisam ser especificadas para definir por completo o sistema.

Vamos olhar pro ponto A, ele tá bem na interseção de 3 fases, então P = 3.

C = 1 para todos os pontos do diagrama, já que o diagrama é da água pura, assim como N, que vai ser sempre igual a 2, já que o diagrama está em função da temperatura e da pressão.

Agora já podemos usar o que sabemos pra calcular F do ponto A.

Quando o número de graus de liberdade é 0, isso indica que as 3 fases estão em equilíbrio, e isso só acontece nesse ponto do diagrama de fases todo, por isso que não existe variável livre.

Agora vamos olhar pro ponto B! Ele está no meio da fase vapor, então P = 1.

Já sabemos C e N, então vamos aplicar a regra de Gibbs:

O número de variáveis livre é 2 justamente porque a fase gasosa representa toda uma região no diagrama, então pra saber que ponto é esse, precisamos dizer exatamente qual é a pressão e a temperatura que queremos.

Agora pro ponto C, temos que P=2 já que está no meio entre a fase líquida e gelo.

Pra esse caso temos 1 variável livre, porque como o ponto tá em cima da linha que divide as duas fases, sabendo a temperatura ou a pressão já é possível encontrar o ponto.