Enunciado
Ciência dos Materiais - Callister - Ciência e Engenharia de Materiais. Uma Introdução- Ed: 8º - Capítulo 12.Problemas de Projetos - Ex. P2
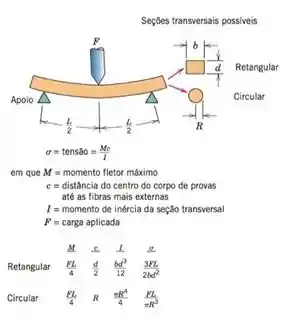
É necessário selecionar um material cerâmico a ser tensionado utilizando um esquema de carregamento em três pontos (Figura 12.32). O corpo de prova deve ter uma seção transversal circular e um raio de e não deve apresentar fratura ou deflexão maior do que em seu centro quando for aplicada uma carga de ). Se a distância entre pontos de apoio é de quais dos materiais da Tabela 12.5 são candidatos? A magnitude da deflexão do ponto central pode ser calculada utilizando a equação fornecida no Problema 12.42. Figura 12.32 abaixo:
Passo 1
Certo galera, vamos lá! A primeira coisa que temos que achar nessa questão, é achar a resistência a flexão. Para isso, temos a equação 12.7b;
Dos materiais da Tabela 12.5, os seguintes possuem comprimentos de flexão superiores a este valor: e .
Passo 2
Para o segundo critério devemos resolver para a magnitude do módulo de elasticidade, , a partir da equação dada no Problema 12.42 onde,
Passo 3
Dos materiais que satisfazem o primeiro critério, apenas e têm módulos de elasticidade superiores a este valor (Tabela 12.5), e, portanto, são possíveis candidatos.
Resposta
e