Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Ciência dos Materiais - Callister - Ciência e Engenharia de Materiais. Uma Introdução- Ed: 8º - Capítulo 8.Perguntas e Problemas - Ex. 21

Suponha que os dados de fadiga para o ferro fundido no Problema 8.20 tenham sido obtidos a partir de ensaios giratórios com dobramento e que uma barra dessa liga deva ser utilizada em um eixo de automóvel que gira a uma velocidade de rotação média de 750   r p m . Determine as vidas máximas, que são admissíveis para uma direção continua, para os seguintes níveis de tensão:

  1. 250   M P a   36.250   p s i ,
  2. 215   M P a   31 . 00 0   p s i ,
  3. 2 0 0   M P a   29.00 0   p s i ,
  4. 1 50   M P a   21.750   p s i .

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

O exercício quer saber quais as vidas máximas admissíveis para cada nível de tensão a partir dos dados da questão anterior.

Vamos marcar no gráfico as tensões e descobrir quais os valores correspondentes de logaritmo do número de ciclos até a falha:

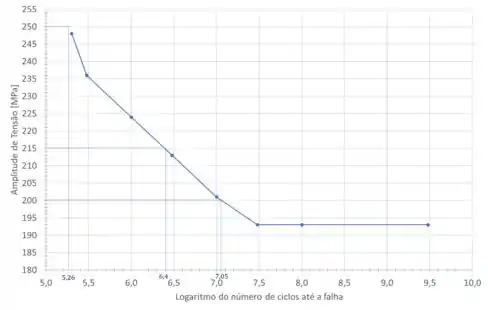
Para o valor de 250   M P a não temos valor então vamos considerar uma linha de tendência e considerar que vale 5,26 .

Para 215   M P a temos 6,4 . E para 200   M P a , temos 7,05 .

Não temos valor para 150   M P a , pois o limite de fadiga é de 193   M P a .

O número de ciclo correspondente para cada valor é de:

log ⁡ N 2 5 0 = 5 , 26

N 2 5 0 = 10 5 , 26

N 2 5 0 = 1,82 × 10 5   c i c l o s

Para 215   M P a :

log ⁡ N 2 1 5 = 6,4

N 2 1 5 = 10 6,4

N 2 1 5 = 2,512 × 10 6   c i c l o s

E para 2 00   M P a :

log ⁡ N 2 0 0 = 7,05

N 2 0 0 = 10 7,05

N 2 0 0 = 1 , 12 × 10 7   c i c l o s

Passo 2

Como nos foi fornecida a velocidade de rotação média, podemos determinar as vidas uteis em termos de tempo.

Se temos 750   r p m , que dizer que a cada minuto temos 750   r o t a ç õ e s .

t = 1 N

Logo:

t = 1 750   m i n / c i c l o

Teremos a seguinte equação:

V i d a   ú t i l   m á x i m a   e m   t e m p o = n ú m e r o   d e   c i c l o s   a t é   a   f a d i g a × p e r í o d o

Passo 3

Agora é só substituir os dados:

  1. Para 250   M P a :

    2. V i d a   ú t i l   m á x i m a   e m   t e m p o = 1,82 × 10 5   c i c l o s × 1 750 m i n c i c l o

    V i d a   ú t i l   m á x i m a   e m   t e m p o = 242,667   m i n

    Em horas temos que:

    V i d a   ú t i l   m á x i m a   e m   t e m p o = 242,667   m i n ⋅ 1 60 h r m i n =   4,04445   h o r a s

  2. Para 2 1 5   M P a :

    3. V i d a   ú t i l   m á x i m a   e m   t e m p o = 2,512 × 10 6   c i c l o s × 1 750 m i n c i c l o

    V i d a   ú t i l   m á x i m a   e m   t e m p o = 2868,2667   m i n

    Em horas temos que:

    V i d a   ú t i l   m á x i m a   e m   t e m p o = 2868,2667   m i n ⋅ 1 60 h r m i n = 47,8   h o r a s

  3. Para 2 0 0   M P a :

    4. V i d a   ú t i l   m á x i m a   e m   t e m p o = 1,12 × 10 7   c i c l o s × 1 750 m i n c i c l o

    V i d a   ú t i l   m á x i m a   e m   t e m p o = 14933,33   m i n

    Em horas temos que:

    V i d a   ú t i l   m á x i m a   e m   t e m p o = 14933,33   m i n ⋅ 1 60 h r m i n = 248,889   h o r a s

  4. Para 150   M P a , o componente não falha por fadiga, portanto se dependesse somente da fadiga a sua vida útil seria infinita.

Resposta

a )   4,04445   h o r a s

b )   47,8   h o r a s

c )   248,889   h o r a s

d )   I n f i n i t a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um ensaio de fadiga foi conduzido tal que a tensão média era de 50MPa (7250psi) e a amplitude de tensão era de 225MPa (32625psi).Calcule os níveis de tensão máximo e mínimo.Calcule a razão entre as te
Cite cinco fatores que podem levar à dispersão em dados da vida em fadiga.
Três corpos de provas de fadiga idênticos (identificados como A , B e C ) são fabricados a partir de uma liga não ferrosa. Cada um é submetido a um dos ciclos de tensão máxima – mínima listados na tab
Os dados de fadiga para um ferro fundido nodular estão dados a seguir:Trace um gráfico S - N (amplitude da tensão em função do logaritmo do número de ciclos até a falha) usando esses dados.Qual é o li