Enunciado
Ciência dos Materiais - Callister - Ciência e Engenharia de Materiais. Uma Introdução- Ed: 8º - Capítulo 8.Perguntas e Problemas - Ex. 20
Os dados de fadiga para um ferro fundido nodular estão dados a seguir:
- Trace um gráfico (amplitude da tensão em função do logaritmo do número de ciclos até a falha) usando esses dados.
- Qual é o limite de resistência à fadiga dessa liga?
- Determine as vidas em fadiga para as amplitudes de tensão de e .
- Estime as resistências à fadiga a e ciclos.
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
O item (a) nos pede para traçar um gráfico da amplitude da tensão em função do logaritmo do número de ciclos até a falha ().
Bom... Nos foi fornecido no enunciado a tabela que nos dá a amplitude de tensão e o numero de ciclos até a falha para cada amplitude.
Devemos então calcular o logaritmo de cada um destes números de ciclos e fazer o nosso gráfico. Podemos utilizar o EXCEL para determinar cada valor de logaritmo e plotar o gráfico:
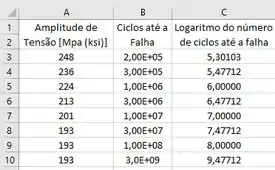
Podemos então plotar o seguinte gráfico:
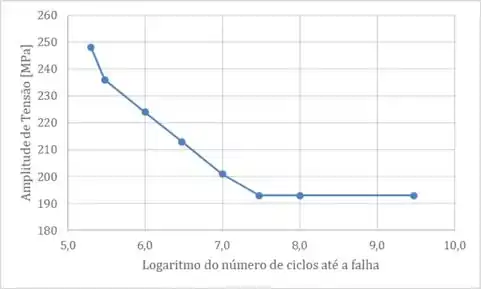
Passo 2
O item (b) nos pergunta qual o limite de resistência à fadiga da liga. O limite de fadiga é o nível de tensão no qual a curva se torna horizontal.
Podemos observar então que este limite será de , que é quando a nossa curva fica constante na horizontal.
O item (c) nos pede o ciclo até a falha para e .
Temos que fazer uma análise do gráfico novamente.
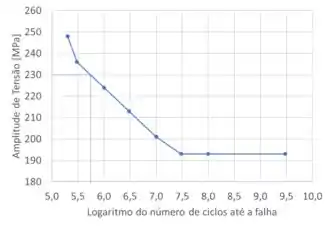
O ponto de logaritmo do número de ciclos até a falha para é de aproximada mente . Portanto:
Para uma amplitude de tensão de , podemos observar que o gráfico não se aplica, pois, este valor é menor que o limite de fadiga, portanto a liga suportaria um número infinito de ciclos sem falhas. Ou seja, para , o corpo não sofre falha por fadiga.
Passo 3
O item (d) nos pede para estimar as resistências à fadiga a e ciclos. Podemos fazer isto a partir da análise gráfica novamente.
Para um valor de ciclos, nem é necessário calcular, pois o mesmo já se encontra na tabela do enunciado e vale .
Para o valor de , temos que seu logaritmo é dado por:
Analisando este valor no gráfico, temos que:
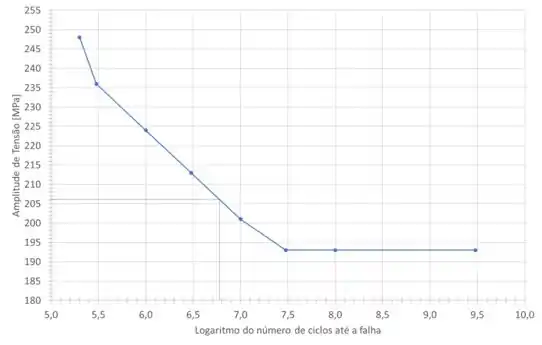
O valor correspondente da amplitude de tensão será de .