Nucleação heterogênea
Teoria
Fala aiiiii pessoal!
Vimos no tópico anterior que para ocorrer a nucleação homogênea uma energia de ativação relacionada a variação de energia livre de Gibbs deve ocorrer para que o primeiro cristal sólido se forme em meio ao líquido.
Mas será que a formação dos cristais sólidos só ocorrerá no meio do líquido?
Para respondermos a essa pergunta, observe na figura abaixo que os gases presentes na água com gás não nucleiam somente do centro. Muito pelo contrário, as bolhas nucleiam também na superfície do vidro e se colocarmos um objeto, por exemplo, uma fatia de limão, dentro dessa água as bolhas irão também nuclear a partir da interface desse limão com a água.
Essa nucleação que ocorre em superfícies e interfaces é denominada nucleação heterogênea.
Para entender esse fenômeno, vamos considerar a nucleação de uma partícula sólida sobre uma superfície plana, a partir de uma fase líquida, conforme figura abaixo.
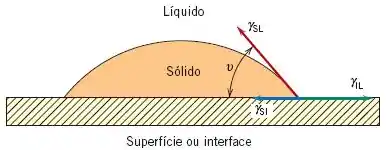
Na figura acima vemos: uma superfície ou uma interface, um líquido solidificando e uma sólido nucleando. Vemos também três energias interfaciais, representadas por vetores.
Fazendo o balanço das forças de tensão superficial no plano da superfície plana, teremos:
Assim, energia de ativação (isto é, a barreira energética) para a nucleação é diminuída quando os núcleos se formam sobre superfícies ou interfaces preexistentes, uma vez que a energia livre de superfície é reduzida, ou seja, é mais fácil a nucleação ocorrer em superfícies ou interfaces que em outros locais.
Energia livre de Gibbs para nucleação heterogênea
Para o calculo da energia livre de Gibbs para nucleação heterogênea usaremos o raio crítico e a energia livre crítica em função do . Vamos ver!
Em que é uma função apenas de e terá valor número entre zero e um.
Assim, teremos:
A expressão acima nos diz que para , a variação de energia livre heterogênea será igual a variação de energia livre homogênea. Para que seja igual a um o sólido não irá nuclear na superfície e sim no meio do liquido.
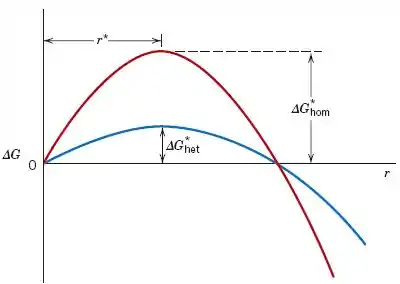
O gráfico acima mostra a curva de variação de energia homogênea e heterogênea. Note que a barreira energética para nucleação homogênea é maior do que a barreira energética para nucleação heterogênea, para um mesmo raio crítico.
Nucleação sólido- sólido
Vimos anteriormente que a nucleação pode ocorrer entre sólido-liquido e também sólido-sólido. Imagine um sólido surgindo dentro de outro sólido, gerando variações de volumes e consequentemente deformações devido essas variações.
A grande maioria das transformações de fase observadas nucleia-se heterogeneamente e, nos sólidos, a tendência para nucleação heterogênea é ainda mais forte. Essas variações aumentam a energia de ativação para a nucleação. Entretanto, contornos de fase, contornos de grão, influenciam nessas deformações, que podem ser cancelados em parte pela nucleação de uma nova fase.
A difusão atômica neste caso é mais rápida ao longo dos contornos de grão do que no cristal diminuindo a barreira energética, característica de uma nucleação heterogênea entre sólidos, ahh é importante deixar claro que para que ocorra essa nucleação é necessário o equilíbrio das tensões interfaciais.
Vamos praticar um pouco para fixar esses conceitos.
Energia livre de Gibbs para nucleação heterogênea ∆ G h e t
Nucleação sólido- sólido
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Defina nucleação heterogênea.
Passo 1
Quando resfriamos um material que está na fase líquida ele não vira sólido todo de uma vez. A primeira etapa do processo de transformação de fase é a nucleação!
A nucleação nada mais é do que a formação de embriões de fase sólida no meio da fase líquida.
Quando esse núcleo sólido se forma no meio de uma matriz contínua, chamamos essa nucleação de nucleação homogênea! Mas e a nucleação heterogênea?
Fica comigo!
Passo 2
A nucleação heterogênea acontece quando a gente tem a formação de núcleos sólidos em superfícies e/ou interfaces!
Dessa forma, os cristais de fase sólida acabam não tendo um formato esférico.
Resposta
A nucleação heterogênea acontece quando a gente tem a formação de núcleos sólidos em superfícies e/ou interfaces.
Exercício Resolvido #2
Elaboração própria
A respeito da nucleação heterogênea, determine a característica correspondente a essa nucleação:
- Ocorre em superfícies pré- existentes
- O núcleo resultante da presença de um substrato possui maior volume e portanto menor número de átomos
- A presença de substrato aumenta o número de átomos, mas não reduz o raio critico
Passo 1
Ocorre em superfícies pré- existentes
Passo 2
O núcleo resultante da presença de um substrato possui menor volume e portanto menor número de átomos
Passo 3
A presença de substrato diminui o número de átomos, mas não reduz o raio critico
Resposta
Alternativa 1
Exercício Resolvido #3
Elaboração própria
Defina sucintamente o que é molhamento e apresente graficamente.
Passo 1
Molhamento é o deslocamento, numa superfície, de um fluído por um outro. Envolve, portanto, três fases, sendo que pelo menos duas delas são fluidas (líquido ou gás). Considere o caso de um líquido que desloca o ar e molha uma superfície sólida, isto é, o líquido se espalha ao longo da superfície sólida, em vez de formar uma gota esférica. Do ponto de vista das energias de superfície
Passo 2
Resposta
Se refere ao ângulo que forma a superfície de um líquido ao entrar em contato com um sólido
Exercício Resolvido #4
Elaboração própria
Sobre o molhamento determine a opção correta:
- Quanto maior é o ângulo de molhamento maior a contribuição do substrato na nucleação.
- O embrião surge na superfície do substrato sob a forma de uma calota esférica, devido à baixa energia de superfície disponível.
- Molhamento, espalhamento e capilaridade são fenômenos físicos relacionados ao comportamento dos materiais e suas propriedades em situações de interação.
Passo 1
Quanto menor é o ângulo de molhamento maior a contribuição do substrato na nucleação.
Passo 2
O embrião surge na superfície do substrato sob a forma de uma calota esférica, devido à energia de superfície disponível.
Passo 3
Molhamento, espalhamento e capilaridade são fenômenos físicos relacionados ao comportamento dos materiais e suas propriedades em situações de interação.
Resposta
Alternativa C
Exercício Resolvido #5
Elaboração própria
A figura abaixo ilustra a diferença do núcleo para as nucleações heterogêneas e homogêneas. Explique o que ocorre abaixo.
Passo 1
A figura ilustra que a superfície a ser criada pela nucleação a partir de um substrato (nucleação heterogênea) é menor, (comparada a da nucleação homogênea) podendo facilitar o processo pois exige menor energia de interface (barreira energética). Observa-se também que o núcleo resultante da presença de um substrato possui menor volume e portanto menor número de átomos.
Resposta
A figura ilustra que a superfície a ser criada pela nucleação a partir de um substrato (nucleação heterogênea) é menor que a nucleação homogênea.
Exercício Resolvido #6
Elaboração própria
A presença de qualquer tipo substrato não é garantia de facilitar a nucleação, então determine e explique qual a característica determinante para que ocorra a nucleação.
Passo 1
A presença de qualquer tipo substrato não é garantia de facilitar a nucleação, pois depende da tensão superficial entre núcleo e o substrato, isto é, depende da molhabilidade entre ambos que, por sua vez, depende da composição química do núcleo e do substrato. Esta molhabilidade pode ser avaliada pelo ângulo.
Resposta
Depende basicamente da tensão superficial entre núcleo e o substrato
Exercício Resolvido #7
Elaboração própria
Sobre a análise termodinâmica, avalia a opção correta:
- A análise termodinâmica realizada para a nucleação homogênea não pode ser aplicada para a nucleação heterogênea
- Substituindo-se a variável energia pela variável número de átomos (N) que constituem um núcleo pode –se avaliar o comportamento termodinâmico.
- Caso haja molhabilidade entre líquido e substrato, a energia crítica para nucleação torna-se menor
Passo 1
A análise termodinâmica realizada para a nucleação homogênea pode ser aplicada para a nucleação heterogênea
Passo 2
A análise termodinâmica realizada para a nucleação homogênea pode ser aplicada para a nucleação heterogênea, porém substituindo-se a variável raio pela variável número de átomos (N) que constituem um núcleo.
Passo 3
Caso haja molhabilidade entre líquido e substrato, a energia crítica para nucleação torna-se menor
Resposta
Alternativa 3
Exercício Resolvido #8
Elaboração própria
A figura abaixo ilustra as parcelas de energia de superfície, volumétrica e total para o caso de nucleação com e sem substrato (índices 2 e 1 respectivamente). Explique o comportamento abaixo.
Passo 1
A presença de um substrato diminui (de DGS1 para DGS2) a energia de interface a ser criada (pois parte desta já existe no substrato), reduzindo a energia crítica total (de DGC1 para DGC2) e portanto o número de átomos necessários para formar o núcleo crítico (de N1 para N2), facilitando a nucleação. (A presença de substrato diminui o número de átomos, mas não diminui o raio crítico).
Resposta
A presença de um substrato diminui (de DGS1 para DGS2) a energia de interface a ser criada (pois parte desta já existe no substrato), reduzindo a energia crítica total (de DGC1 para DGC2) e portanto o número de átomos necessários para formar o núcleo crítico (de N1 para N2), facilitando a nucleação. (A presença de substrato diminui o número de átomos, mas não diminui o raio crítico).