Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Comandos de entradas e saídas de dados

Ver Teoria
Exercício 61234578

Enunciado

Seja o conjunto A = { 1,12,31,54 } . Construa em código Matlab a função f : A , B : x → x 3 - x 2 e forneça um conjunto B compatível com a definição de f .

Passo 1

A questão é que ela dá uma entrada de dados da forma vetor e pede para que elabore um programa em Matlab que execute a operação que é pegar cada elemento do vetor e elevar ele ao cubo e depois o mesmo elemento ao quadrado.

Após isso é subtrair x 3 - x 2 nos dando o vetor B, o algoritmo para a resolução do problema é dado por:

1 - E n t r a d a   d e   d a d o s   ( e n t r a r   o s   v a l o r e s )

2 - C r i a ç ã o   d o s   V e t o r

3 - D e t e r m i n a r   x 3 - x 2

4 - I m p r i m i r   c a d a   r e s u l t a d o s   n a   f o r m a   d e   v e t o r

A sacada daqui é lembrar que para realizar uma operação de cada elemento do vetor é preciso colocar o ponto antes da operação tipo X 3 em linguagem de programação para cada elemento ficaria X.^3

Passo 2

Para inserir o programa no Matlab, precisamos transformar o algoritmo em linguagem de programação, então:

X 1 = i n p u t ( ' d i g i t e   o   v a l o r   d e   X 1   =   ' ) ;

X 2 = i n p u t ( ' d i g i t e   o   v a l o r   d e   X 2   =   ' ) ;

X 3 = i n p u t ( ' d i g i t e   o   v a l o r   d e   X 3   =   ' ) ;

X 4 = i n p u t ( ' d i g i t e   o   v a l o r   d e   X 4   =   ' ) ;

X = [ X 1 ; X 2 ; X 3 ; X 4 ] ;

B = X . ^ 3 - X . ^ 2

f p r i n t f ( ' O   e l e m e n t o   X 1   d e   B   é   i g u a l   a   % f   \ n ' , B ( 1,1 ) )

f p r i n t f ( ' O   e l e m e n t o   X 2   d e   B   é   i g u a l   a   % f   \ n ' , B ( 2,1 ) )

f p r i n t f ( ' O   e l e m e n t o   X 2   d e   B   é   i g u a l   a   % f   \ n ' , B ( 3,1 ) )

f p r i n t f ( ' O   e l e m e n t o   X 2   d e   B   é   i g u a l   a   % f   \ n ' , B ( 4,1 ) )

Passo 3

O programa no Matlab se torna:

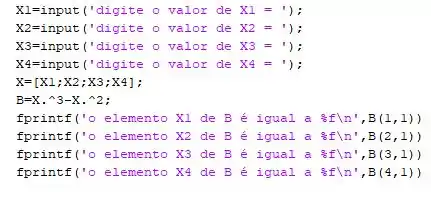
Passo 4

Ao testar teremos assim:

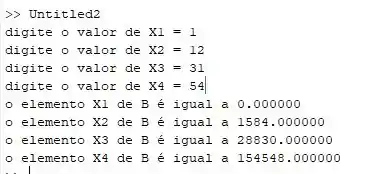
Resposta

Ei, a resposta está no passo a passo :)