Comandos de entradas e saídas de dados
Produzido por Gustavo BarbosaTeoria
Para que isso serve?
Opa, iae está tudo bem?
Hoje vamos conversar um pouco sobre os comandos de entrada e saída de dados.
Quando estamos criando algum algoritmo sempre precisamos começar de um ponto zero e esse ponto se chama entrada de dados.
Uma vez que todo o comando do algoritmo é executado, uma informação precisa sair da sua rotina e esses são os comandos de saída de dados.
Mas qual a importância de saber disso né?
Vamos imaginar que você trabalha como atendente de farmácia, chega um cliente, mas ele não fala nada.
Como você saberia qual remédio pegar na despensa?
Se o cliente não falar nada, você não tem como proceder o atendimento e logo não tem como entregar o produto que o cliente deseja. Sendo assim, se não existe uma entrada de dados, não tem como o código proceder e o algoritmo não cumpre seu objetivo.
De uma forma similar, se ele falasse o produto que deseja e você fosse na despensa buscar, mas não entregasse a ele, o atendimento não se completaria. Sem a saída de dados, a rotina não teria fim.

E que comando são esses né? Então vamos laaaaaa
Comandos de entrada de dados.
Como já conversamos, os comandos de entradas de dados são os pontos iniciais de qualquer algoritmo. A utilização de um comando de entrada de dados possibilita que seu código possa solicitar e atribuir os dados do problema via teclado.
Basicamente no Matlab a função que realiza esse trabalho é a função input. Para entendermos como ela funciona, vamos anexar uma variável a qualquer com o comando input.
Basta abrir a aba new script e inserir o seguinte código:
Salvando o arquivo e executando o código, deve mostrar algo assim:

Ou seja, agora o Matlab pergunta qual valor será indexado à variável.
Repara que podemos escrever o que quisermos na mensagem que aparece ao usuário: chamamos a variável de no programa, mas pedimos ao usuário pra digitar o valor de .
Então fica ligado, o nome da variável tem que ser claro pra você e pras outras pessoas que estão mexendo no código, já a mensagem exibida tem que deixar claro pro usuário do programa o que tá sendo pedido.
Logo, de uma forma geral a sintaxe é dada por:
Comandos de saída de dados.
Quando estamos falando dos comandos de saídas de dados para o Matlab temos dois, a função disp e a função fprintf.
A diferença entre essas funções é que a possibilita uma melhor formatação da saída de dados em relação a função .
Vamos continuar o exemplo passado:
Aproveitando o código anterior vamos inserir mais uma linha que é:
Se você digitou tudo certinho, ao inserir a variável no command window, vemos:

Ou seja, após inserir a variável, o command window imprimiu o valor dela sendo 10.
Só que fica uma coisa desorganizada, meio solta né? Imagine você com um código que tem várias informações de saída, essa função não fica muito legal.
Por isso existe a função , que tem alguns detalhes adicionais que auxiliam na formatação da saída de dados.
Mas antes de falar isso vamos utilizar o exemplo anterior e escrever a seguinte linha:
Ao digitar tudo certinho, a saída de dados agora fica assim:

Ou seja, a função possibilita também a inserção de textos e sua sintaxe geral é dada por:
Porém na linha que escrevemos tem um , e você deve estar se perguntando o que é isso né?
Na função você precisa indicar qual tipo de variável ele vai imprimir quando estiver escrevendo a mensagem da impressão.
Nesse exemplo, eu pedi para ele imprimir uma variável do tipo , que é uma variável flutuante, por isso ela foi impressa de forma decimal.
Sempre que escrever a mensagem, na posição que se deseja imprimir a variável no texto você precisa indicar que tipo de variável ela é.
Por exemplo vamos supor que queremos imprimir uma data, vamos escrever na aba new script o seguinte código
Ao executar o código, o Matlab irá mostrar para você a seguinte informação:

Ou seja, eu queria imprimir os valores das datas após o ponto, então onde iria imprimir eles eu indiquei que a impressão é do tipo inteira com a informação %i.
Logo a função permite uma formatação bem mais flexível da saída de dados. E para isso, você precisa apenas saber os seguintes códigos:

Para finalizar vamos realizar um problema mais completinho:
Exemplo: Escreva um código que, dado dois valores, retorne a média desses valores.
Primeiramente vamos escrever o algoritmo para termos uma ideia do que se passa no código:
- Entrada de dados ( e )
- Cálculo da média com a função
- Saída de dados com o valor da média.
Uma vez que o algoritmo está pronto, vamos escrever o código!
Primeiramente precisamos inserir a entrada de dados:
Agora que criamos a entrada de dados, vamos criar a função média:
Pra fechar, vamos criar a saída de dados:
Então seu código vai ficar algo assim:

Salvando o arquivo e executando, temos:
Iae, curtiu o papinho? Essa parte é bem prática, então não esqueça de olhar os exercícios que selecionamos para você!
Então ficamos por aqui e até a próxima!
Comandos de entrada de dados.
Comandos de saída de dados.
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
Elabore um código em Matlab que leia do teclado três valores e imprima o maior e o menor entre eles.
Dica: utilize as funções Max e Min do Matlab, elas selecionam o maior e o menor vetor de uma certa matriz.
Passo 1
A ideia é elaborar um programa simples para ler três números e imprimir o maior e o menor entre eles.
O foco aqui é mostrar como começar a praticar com as funções de entrada e saída de dados.
Então o algoritmo é simplesmente:
- Entrada de dados
- Criação de um vetor único com os 3 números
- Seleção do maior e do menor valor
- Impressão das respostas.
Porque criamos um vetor no passo 2? Para podermos usar os comandos e . Esses comandos devem ter um vetor como argumento. Então eles procuram nesse vetor, o maior e o menor termos, respectivamente.
Agora que sabemos do algoritmo vamos implementar na linguagem computacional.
Passo 2
Primeiramente precisamos da entrada de dados que fica.
Após isso colocamos o código que vai executar o que se pede:
Agora vamos fazer o passo 2 do algoritmo, criar um vetor único com os 3 números. Pra isso, escrevemos as 3 variáveis dentro de colchetes, separadas por espaços. E chamamos esse vetor de .
Agora que temos um vetor com todos os números podemos usar os comandos e para achar o maior e o menor termos. Vamos chamar o valor máximo de e o valor mínimo de .
E agora a saída de dados com a impressão
Passo 3
Uma vez escrito o código, ele deve estar no seu Matlab mais ou menos assim:

Ao executar o código deve mostrar algo assim:

Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #2
“Elaboração Própria”
Escreva um programa em MATLAB para calcular e imprimir os valores de Y para um dado valor de X fornecido pelo teclado. A expressão que define Y em função de X é dada por:
Passo 1
A questão pede para elaborar um programa em Matlab que dado algum número X de entrada forneça uma saída Y que é dada pela função acima.
Criando o algoritmo para a rotina temos que:
1-Entrada de dados (X).
2- Cálculo do Y através da função.
3-Impressão de saída.
Passo 2
Para inserir o programa no Matlab, precisamos transformar o algoritmo em linguagem de programação, então:
X=input(‘Digite o valor de X = ‘);
Y=1/X-4.3*log(X)+X^4;
fprintf(‘O valor de Y calculado pela função é %f’,Y)
Passo 3
O programa no Matlab se torna:

Digitando X=5 para testar teremos algo assim:
![]()
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #3
“Elaboração Própria”
Seja o conjunto . Construa em código Matlab a função e forneça um conjunto B compatível com a definição de .
Passo 1
A questão é que ela dá uma entrada de dados da forma vetor e pede para que elabore um programa em Matlab que execute a operação que é pegar cada elemento do vetor e elevar ele ao cubo e depois o mesmo elemento ao quadrado.
Após isso é subtrair nos dando o vetor B, o algoritmo para a resolução do problema é dado por:
A sacada daqui é lembrar que para realizar uma operação de cada elemento do vetor é preciso colocar o ponto antes da operação tipo em linguagem de programação para cada elemento ficaria X.^3
Passo 2
Para inserir o programa no Matlab, precisamos transformar o algoritmo em linguagem de programação, então:
Passo 3
O programa no Matlab se torna:
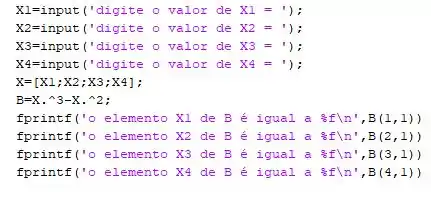
Passo 4
Ao testar teremos assim:
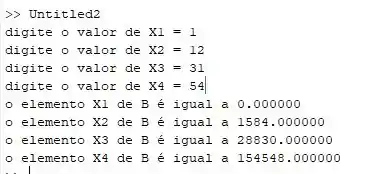
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #4
“Elaboração Própria”
Leia dois vetores de três elementos do teclado, e calcule o produto escalar e o produto vetorial dado por eles:
Produto escalar:
Produto Vetorial: )
Passo 1
A questão pede para elaborar um programa que calcule tanto o produto vetorial quanto o produto escalar dados dois vetores, a questão fornece as equações para o produto vetorial e o produto escalar, bastando apenas formular o algoritmo e implementá-lo em linguagem de programação no Matlab.
O Algoritmo proposto será:
1-Entrada de dados (elementos de u e elementos de v)
2-Cálculo do produto escalar
3-Cálculo do produto vetorial
4-Impressão dos resultados
Passo 2
Para inserir o programa no Matlab, precisamos transformar o algoritmo em linguagem de programação, então:
Passo 3
O programa no Matlab se torna:
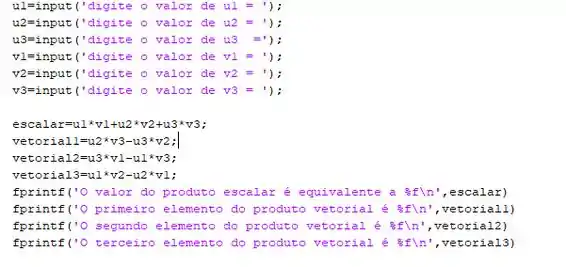
Passo 4
Ao testar teremos assim utilizando os valores abaixo temos:

Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #5
“Elaboração Própria”
Sabendo-se que o vetor X assume os seguintes números: 3, 5, 6, 6, 7, 10, 12. Escreva um programa em Matlab capaz de:
- Ler os valores do vetor X;
- Determinar a soma do vetor X;
- Determinar a média aritmética do vetor X
- Determinar a média aritmética geométrica do vetor X
- Imprimir os resultados.
Passo 1
Fala, pessoal. Nessa questão, precisamos ler 7 valores que formam um vetor X. E então calcular sua soma, média aritmética e média aritmética geométrica. Para isso precisaremos de duas funções do matlab.
Primeira é length que diz o número de elementos de um vetor ou de uma matriz e de como criar um vetor no Matlab. Precisamos criar um vetor para podermos usar a função .
O algoritmo é dado por:
Passo 2
Para inserir o programa no Matlab, precisamos transformar o algoritmo em linguagem de programação.
O primeiro passo é a entrada de dados. Vamos usar a função input para pedir ao usuário os valores das variáveis. Dentro do parênteses à direita do input, escrevemos uma mensagem que o usuário vai receber. O que for digitado pelo usuário, a cada linha, é o valor que será atribuído à variável.
Agora vamos criar um vetor com todos os 7 números. Pra isso escrevemos as variáveis dentro de colchetes, separadas por ponto e vírgula.
Tendo um vetor, podemos usar a função
Vamos calcular a soma dos 7 números e, com ela, as médias aritmética e aritmética geométrica.
Por fim, usamos para imprimir uma mensagem para o usuário.
Passo 3
O programa no Matlab se torna:

Passo 4
Ao testar teremos assim:

Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #6
“Elaboração Própria”
O saldo de uma caderneta de poupança, após t anos, feito um investimento inicial e sendo a taxa de juros anual em , é dado por:
Escreva um programa em Matlab que a partir de uma entrada de dados forneça o saldo dessa caderneta como a saída de dados.
Passo 1
Bem, essa questão pede o cálculo de um juro composto a partir de uma entrada de dados, em geral, os juros são calculados por expressões similares a essa.
Quem nunca atrasou uma conta de cartão de crédito né?
Aquele valorzinho que o banco cobra a mais é calculado através de fórmulas similares a essa, então basicamente vamos alimentar essa fórmula para realizar a operação que é o cálculo do saldo e imprimir esse valor na workspace.
Mas quais são as variáveis de entrada?
Bem, aqui as variáveis de entrada são as variáveis que alimentam a nossa fórmula.
Que corresponde às variáveis e como variável de saída temos o .
Sendo assim, temos que o nosso codigozinho é composto por três partes:
- Entrada de dados
- Cálculo do P
- Saída de dados
Passo 2
Agora que já elaboramos toda essa discussão do passo 1, vamos colocar a mão na massa.
Primeiramente precisamos implementar as entradas de dados, para isso vamos utilizar uma função do Matlab chamada de função .
Ela tem uma habilidade muito especial que é memorizar na workspace algum valor que iremos fornecer pelo nosso teclado.
A sintaxe é bem simples, vamos começar relembrando a sintaxe criamos a variável
Aqui podemos analisar que depois de chamar a função input, entre parênteses escrevemos um textinho.
Esse textinho tem como função apenas deixar a janela de command window mais organizadinha para você saber qual variável vai digitar naquele momento, ok?
Consequentemente as demais são:
Aqui vamos realizar nossa operação:
E para finalizar vamos compor a saída de dados, para isso vamos utilizar a função printf.
Essa função fprintf pega uma variável na workspace e imprime na nossa janela de command window.
A vantagem de utilizar a função fprintf é que podemos organizar a saída de dados com algum textinho, por exemplo.
Então a saída de dados fica assim:
Dentro da função nos inserimos dois para indicar qual o tipo de variável vai ser impressa, o f vai indicar que a saída é float e elas vão ser impressas no lugar dos %f.
Após indicar quais os tipos e em que localidade do texto elas vão ser imprimidas temos que indicar quais variáveis são, o primeiro %f é o P e o segundo é o t.
Sendo assim, primeiramente imprime-se o P e depois o t.
Digitando tudo certinho seu código deve ficar algo assim:

Passo 3
Para realização do teste vamos utilizar os seguintes valores:
Temos um valor de equivalente a:

Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #7
“Elaboração Própria”
Realize a seguinte operação Matemática no Matlab:
A função deve receber a variável em graus, converter para radianos e retornar R como uma saída de dados.
Passo 1
Opa galera, essa questão pede para calcular o valor da posição de uma partícula a partir da função vetorial dada e de uma entrada de dados.
Para isso vamos criar uma entrada de dados, onde o programinha vai realizar algumas operações sob a entrada de dados para o final imprimir a saída de dados.
Mas quais são as variáveis de entrada e de saída?
Nessa questão as variáveis de entrada são as variáveis que alimentam a nossa fórmula. Que corresponde a variável e como variável de saída temos o .
Sendo assim, temos que o nosso codigozinho é composto por três partes:
- Entrada de dados
- Cálculo do R
- Saída de dados
Passo 2
Agora que já elaboramos toda essa discussão no passo 1, vamos colocar a mão na massa.
Primeiramente precisamos implementar as entradas de dados, para isso vamos utilizar uma função do Matlab chamada de função .
Ela tem uma habilidade muito especial que é memorizar na workspace algum valor que iremos fornecer pelo nosso teclado.
A sintaxe é bem simples, vamos começar relembrando a sintaxe criamos a variável
Aqui podemos analisar que depois de chamar a função input, entre parênteses escrevemos um textinho.
Esse textinho tem como função apenas deixar a janela de command window mais organizadinha para você saber qual variável vai digitar naquele momento, ok?
Aqui vamos realizar nossa operação:
Primeiramente vamos converter o ângulo de graus em radianos através da seguinte formulinha:
Para implementar o Raio vamos dividir ele em duas componentes, uma que é a componente e outra que é a componente
E para finalizar vamos compor a saída de dados, para isso vamos utilizar a função printf.
Essa função printf pega uma variável na workspace e imprime na nossa janela de command window.
A vantagem de utilizar a função fprintf é que podemos organizar a saída de dados com algum textinho, por exemplo.
Então a saída de dados fica assim:
Dentro da função nos inserimos dois para indicar qual o tipo de variável vai ser impressa, o f vai indicar que a saída é float e elas vão ser impressa no lugar dos .
Após indicar quais os tipos e em que localidade do texto elas vão ser imprimidas temos que indicar quais variáveis são, o primeiro é o e o segundo é o .
Digitando tudo certinho seu código deve ficar algo assim:

Passo 3
Para realização do teste vamos utilizar o seguinte valor:
Temos um valor de equivalente a:

Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #8
“Elaboração Própria”
Sistemas de filtração para o tratamento de sinais são alguns dos artifícios mais importantes dentro da engenharia.
São eles que cancelam os ruídos, as perturbações e vários outros problemas que impossibilitam ou dificultam a transmissão do sinal.
Por exemplo imagina você ligar para seu amigo que está a 300 km de distância de você e conseguir ouvir ele normalmente, sendo que a onda eletromagnética está passando por diversos meios e caminhando por no mínimo 300 Km de distância, e você consegue ouvir ele claramente, como se ele tivesse do seu lado.
Isso é possível devido a equipamentos de filtragem nos aparelhos de celular.
Sendo assim vamos para a questão.
Um filtro passa – faixa permite a passagem de frequências compreendidas em uma faixa entre duas frequências limites, nesse filtro, o ganho de tensão é dado por:
O esquema do filtro é dado por:

Obs:
Passo 1
Opa galera, essa questão pede para calcular o valor do ganho de tensão desse filtro a partir de uma entrada de dados, esse ganho de tensão é dado pelo valor de que corresponde à razão das tensões antes e após ao filtro.
Para isso vamos criar uma entrada de dados, onde o programinha vai realizar algumas operações sob a entrada de dados para ao final imprimir a saída de dados.
Mas quais são as variáveis de entrada e de saída?
Nessa questão as variáveis de entrada são as variáveis do projeto do filtro, em geral, um engenheiro dispõe dos valores das constantes dos componentes eletrônicos que compõem o circuito.
Nesse sentido, as variáveis que o engenheiro conhece são a capacitância, e indutância, a resistência e a frequência angular da corrente alternada e como a saída de dados temos o ganho de tensão.
Sendo assim, temos que o nosso codigozinho é composto por três partes:
- Entrada de dados
- Cálculo do RV
- Saída de dados
Passo 2
Agora que já elaboramos toda essa discussão no passo 1, vamos colocar a mão na massa.
Primeiramente precisamos implementar as entradas de dados, para isso vamos utilizar uma função do Matlab chamada de função .
Ela tem uma habilidade muito especial que é memorizar na workspace algum valor que iremos fornecer pelo nosso teclado.
A sintaxe é bem simples, vamos começar relembrando a sintaxe criamos a variável
Aqui podemos analisar que depois de chamar a função input, entre parênteses escrevemos um textinho.
Esse textinho tem como função apenas deixar a janela de command window mais organizadinha para você saber qual variável vai digitar naquele momento, ok?
Consequentemente as demais entradas de dados correspondem a:
Passo 3
Após isso vamos realizar nossa operação que é:
E para finalizar vamos compor a saída de dados, para isso vamos utilizar a função fprintf. Essa função fprintf pega uma variável na workspace e imprime na nossa janela de command window. A vantagem de utilizar a função fprintf é que podemos organizar a saída de dados com algum textinho.
Então a saída de dados fica assim:
Dentro da função nos inserimos um para indicar qual o tipo de variável vai ser impressa, o f vai indicar que a saída é float e a variável vai ser impressa no lugar do.
Digitando tudo certinho seu código deve ficar algo assim:

Resposta
