Uma amostra seca de carvão apresenta a seguinte análise mássica de: de carbono , de hidrogênio , de oxigênio , de nitrogênio , de enxofre e de cinzas não combustíveis.
A amostra deste carvão é queimada com ar seco, formando gás carbônico , nitrogênio , vapor d’água e dióxido e enxofre . Considerando que os produtos de combustão se encontram a pressão total de , determine a temperatura do ponto de orvalho dos produtos.
Passo 1
Oooi, pessoal! Esse enunciado é cheio de informação, né? Ele fala sobre uma reação de combustão que envolve tantas moléculas que fica difícil entender quais são os reagentes e os produtos. Por isso, nosso primeiro passo deve ser escrever a equação química da combustão, mostrando os reagentes e produtos sem os valores dos coeficientes estequiométricos..

O enuciado diz que , , , e reagem com ar seco que é composto por uma parte de e partes de . Como essas moléculas reagem, elas são os reagentes, certo?
O enunciado também diz que , , e são produzidos pela reação. Logo, essas moléculas são os produtos. Colocando os reagentes na esquerda e produtos na direita:
, , , , , , , , e são os coeficientes estequiométricos da equação química! As cinzas não estão nessa equação, porque não participam da reação! Esses coeficientes estequiométricos precisam ser encontrados para encontrarmos a temperatura do ponto de orvalho dos produtos. Ela é a temperatura de saturação da água na pressão parcial da água.
onde é a pressão parcial do vapor d’água nos produtos. Essa pressão parcial é igual à pressão total dos produtos multiplicada pela fraçõ molar da água nos produtos.
A fração molar de água é igual à quantidade de de água nos produtos dividida pela quantidade de total dos produtos .
é a soma entre , , e . Esses coeficientes dos produtos são determinados através do balanço da equação química que começaremos a fazer no próximo passo.
Passo 2
O primeiro passo para fazer o balanço de uma equação com combustível misturado é determinar a quantidade de (no nosso caso , , , e ) dos componentes do combustível. Calcularemos , supondo que de combustível é queimado. Pra isso, achamos primeiro a massa de multiplicando pelos de no combustível.
Da mesma forma, achamos a massa de , multiplicando pelos de no combustível. A massa de é encontarda, multiplicando pelos de .
Fazemos o mesmo com e . Suas massas e são calculadas, multiplicando a massa de do combustível todo pelas suas porcentagens mássicas dadas pelo enunciado.
Nós calculamos as massas pro caso de de combustível serem queimados, mas tanto faz a quantidade de combustível que supomos ser queimada. Ela não interfere no cálculo de !
Agora, para achar a quantidade de de nos reagentes, dividimos pela massa molar do carbono que vale .
é encontrado, dividindo pela massa molar do hidrogênio que vale segundo as tabelas termodinâmicas de gases.
Encontramos a quantidade de de presente no combustível, dividindo pela massa molar do que vale .
Por fim, achamos e , dividindo e pelas massas molares de e de .
Com esses coeficientes já somos capazes de achar os coeficientes restantes!
Passo 3
Determinamos o coeficiente estequiométrico , fazendo o balanço do carbono . Para a quantidade de ficar balanceada, os de presentes nos produtos precisam ser iguais aos de presentes nos reagentes. A equação química é mostrada abaixo pra enxergarmos melhor.
Da mesma forma, achamos , fazendo o balanço do hidrogênio . Os do produto têm que ser iguais aos do reagente.
também pode ser encontrado logo, fazendo o balanço do enxofre . Para a quantidade de ficar balanceada, os de dos produtos devem ser iguais aos de dos reagentes.
Agora podemos achar o coeficiente , fazendo o balanço de oxigênio . Os de dos reagentes devem ser iguais aos de dos produtos.
Com esses coeficientes em mãos, podemos finalmente calcular o coeficiente através do balanço de . Os de dos reagentes têm que ser iguais aos de dos produtos!
Agora sim estamos aptos a calcular a fração molar da água pra achar no próximo passo!
Passo 4
Como , , e são os produtos da combustão, a quantidade total de dos produtos é a soma das quantidades de de , , e .
Substituindo essa quantidade de na fórmula de :
Com esse valor, somos capazes de achar a pressão parcial do vapor d’água nos produtos.
A temperatura de ponto de orvalho é a temperatura de saturação da água a . Logo, temos que usar a tabela termodinâmica da água pra achar . Como essa tabela não possui o valor de temperatura de saturação para esse valor de pressão, nós temos que interpolar a temperatura, usando os valores de temperatura de saturação a e .
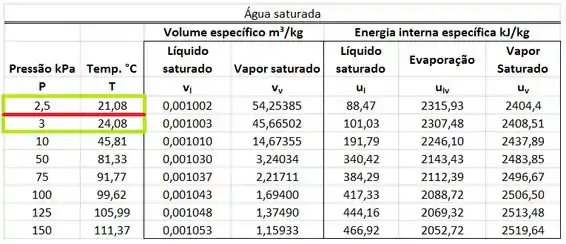
Aeeeee! Achamos o valor da temperatura de ponto de orvalho dos produtos! Ela vale ! Isso quer dizer que se a gente resfriar os produtos gerados pela combustão a pressão constante, quando eles chegarem na temperatura de , a água dos produtos começará a condensar.