Uma coluna de recheio com cerâmicas Intalox de deve ser construída para tratar: ) de entrada de gás por hora. O conteúdo de amônia do gás que entra é de em volume. Água sem amônia é usada como adsorvente. A temperatura é de e a pressão é de . A razão entre o fluxo de gás e o fluxo de líquido é de de gás por de líquido.
Se a velocidade do gás deve ser metade da velocidade de inundação, qual deveria ser o diâmetro da coluna?
Passo 1
Oi oiee, tudo bem? Nessa questão nós temos uma coluna com ) de entrada de gás por hora contendo amônia em volume. Considerando que a coluna está nas seguintes condições,
E que,
Precisamos calcular o diâmetro da coluna onde a velocidade do gás é a metade da velocidade de inundação. Então vamos lá!
Passo 2
Temos que o peso molecular médio do gás que entra é,
Então,
Passo 3
O enunciado nos disse que,
Ou seja,
ou
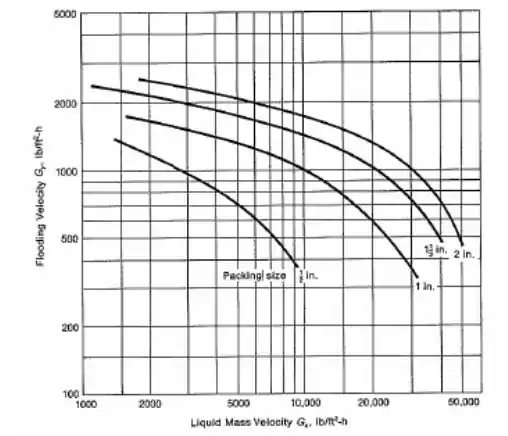
Além disso, nos disse que as cerâmicas têm . Logo, com o gráfico podemos encontrar o valor das vazões no ponto em que as vazões são iguais para o recheio de

Cruzando essas informações encontramos que
Passo 4
Como a velocidade do gás deve ser metade da velocidade de inundação temos,
Assim o fluxo total do gás é,
Então a área da seção transversal da torre é,
Como a área é,
Logo,