Determinação do Diâmetro da Coluna Recheada
Teoria
Introdução
Faaaaala aiii, tudo certinho? Agora nós vamos dar um pouco mais de atenção para a coluna recheada especificamente e falar sobre o diâmetro dela.
Primeira coisa que temos que ter em mente é que a coluna recheada e irrigada por uma determinada vazão de líquido tem um limite superior para vazão de gás. E a velocidade do gás correspondente a este limite é chamada de velocidade de inundação (ou flooding).
O fluxo ou velocidade de inundação pode ser obtida por meio gráfico baseada na correlação de Sherwood. E na hora de calcular esse fluxo é comum assumir uma certa porcentagem do fluxo de inundação para o fluxo de operação do gás. Para que nós tenhamos a famosa margem de segurança, beleza?
Então vamos ver como funciona esse gráfico.
Gráfico da Correlação de Sherwood
Neste gráfico, a abscissa (eixo horizontal) é calculada à partir dos fluxos de processo (líquido e gás) e a ordenada(eixo vertical) à partir do ponto de inundação correspondente. O fluxo de operação para o gás, em princípio, deve ser calculada pela otimização da torre.
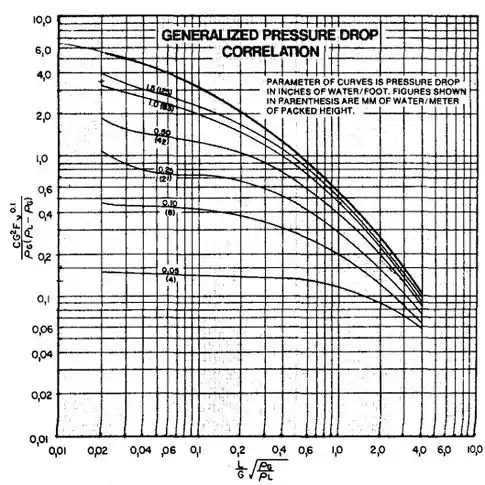
Calma calma calma, eu sei que o gráfico é feio, mas não desanima, vamos apender ele juntinhos
Abscissa:
Onde,
E para a ordenada temos,
Onde,
Lembrando que,
E sabendo que, normalmente, vamos considerar,
Diâmetro da coluna
Vamos agora montar um passo a passo do que precisamos fazer para definir o diâmetro da coluna, beleza?
1°) Vamos determinar a abcissa a partir das condições de topo ou de fundo da torre;
2°) Vamos localizar no gráfico o ponto de inundação (flooding);
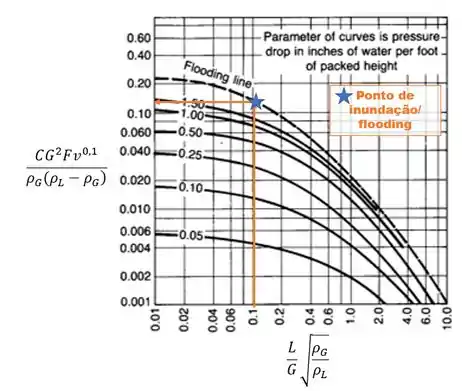
3°) Determinar a ordenada e daí ( de flooding);
4°) Calcular (“op” de operação) arbitrando um percentual da razão de flooding (varia entre 40 e 80% dependendo do sistema);
5°) Com calcular o diâmetro,
Onde,
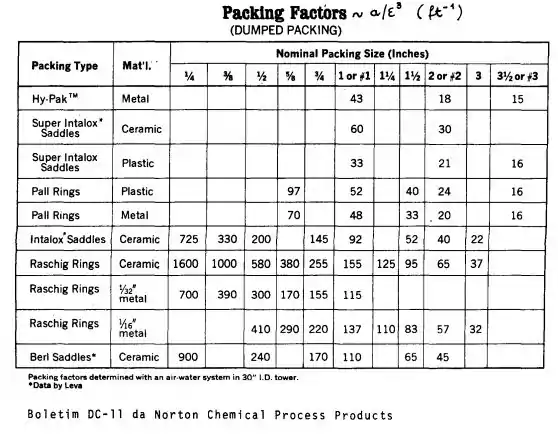
Caracterização do recheio
O recheio é caracterizado pelo diâmetro nominal (, área específica e porosidade e porosidade e é representado por Beleza, mas ai você me pergunta: como vamos definir ele?
Para isso temos uma bela tabela!! Saca só,
Beleza? Agora vamos para os exercícios 😊
Gráfico da Correlação de Sherwood
Diâmetro da coluna
Caracterização do recheio
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Explique o conceito de velocidade de inundação ou flooding.
Passo 1
Heyyy, tudo bem? Vamos iniciar nossos exercícios sobre o diâmetro da coluna recheada vendo um conceito importante que é o de velocidade de inundação.
Passo 2
Velocidade de inundação ou flooding é a velocidade do gás correspondente ao limite superior para vazão de gás em uma coluna recheada.
Esse fluxo ou velocidade de inundação pode ser obtida por meio gráfico baseada na correlação de Sherwood. E na hora de calcular esse fluxo é comum assumir uma certa porcentagem do fluxo de inundação para o fluxo de operação do gás.
Resposta
Velocidade de inundação ou flooding é a velocidade do gás correspondente ao limite superior para vazão de gás em uma coluna recheada.
Exercício Resolvido #2
Elaboração própria
Determine o ponto de inundação de uma coluna recheada sabendo que a razão entre líquido e gás é e dados:
Passo 1
Faaaaala aíii, tudo certinho? Nessa questão nós queremos encontrar o ponto de inundação, ou seja, vamos ter que usar esse gráfico bem aqui:
Repara que o enunciado já nos deu o eixo
Então só precisamos encontrar o valor do eixo para rebater na curva encontrando nosso ponto de inundação 😉
Passo 2
O enunciado nos disse que,
E nos forneceu,
Jogando esses dados na equação do eixo temos,
Passo 3
Cruzando agora essas informações no gráfico temos,
Logo, a velocidade de inundação/ponto de inundação é,
Resposta
Exercício Resolvido #3
Adaptado – Exemplo 22.1, Unit Operation of Chemical Engineering, quinta edição, McCabe W. L., et all.
Uma coluna de recheio com cerâmicas Intalox de deve ser construída para tratar: ) de entrada de gás por hora. O conteúdo de amônia do gás que entra é de em volume. Água sem amônia é usada como adsorvente. A temperatura é de e a pressão é de . A razão entre o fluxo de gás e o fluxo de líquido é de de gás por de líquido.
Se a velocidade do gás deve ser metade da velocidade de inundação, qual deveria ser o diâmetro da coluna?
Passo 1
Oi oiee, tudo bem? Nessa questão nós temos uma coluna com ) de entrada de gás por hora contendo amônia em volume. Considerando que a coluna está nas seguintes condições,
E que,
Precisamos calcular o diâmetro da coluna onde a velocidade do gás é a metade da velocidade de inundação. Então vamos lá!
Passo 2
Temos que o peso molecular médio do gás que entra é,
Então,
Passo 3
O enunciado nos disse que,
Ou seja,
ou
Além disso, nos disse que as cerâmicas têm . Logo, com o gráfico podemos encontrar o valor das vazões no ponto em que as vazões são iguais para o recheio de
Cruzando essas informações encontramos que
Passo 4
Como a velocidade do gás deve ser metade da velocidade de inundação temos,
Assim o fluxo total do gás é,
Então a área da seção transversal da torre é,
Como a área é,
Logo,
Resposta
Exercício Resolvido #4
Adaptado – Exemplo 22.1, Unit Operation of Chemical Engineering, quinta edição, McCabe W. L., et all.
Uma coluna de recheio com cerâmicas Intalox de deve ser construída para tratar: ) de entrada de gás por hora. O conteúdo de amônia do gás que entra é de em volume. Água sem amônia é usada como adsorvente. A temperatura é de e a pressão é de . A razão entre o fluxo de gás e o fluxo de líquido é de de gás por de líquido.
Qual é a queda de pressão se a sessão do recheio tiver de altura?
Passo 1
Oi oiee, tudo bem? Nessa questão nós temos uma coluna com ) de entrada de gás por hora contendo amônia em volume. Considerando que a coluna está nas seguintes condições,
E que,
A partir disso vamos calcular a queda de pressão se a sessão do recheio tiver de altura. Então vamos lá!
Passo 2
Temos que o peso molecular médio do gás que entra é,
Então,
Passo 3
O enunciado nos disse que,
Ou seja,
ou
Logo, com o gráfico podemos encontrar o valor da a queda de pressão:
Então, a queda de pressão para é,
A queda de pressão total é então,