Tensão Trifásica
Teoria
Os circuitos trifásicos, o famoso
Como funciona a Tensão Trifásica
Em um sistema trifásico equilibrado as tensões são iguais em amplitude, porém estão defasadas em 120°. Se liga nesse gráfico abaixo:
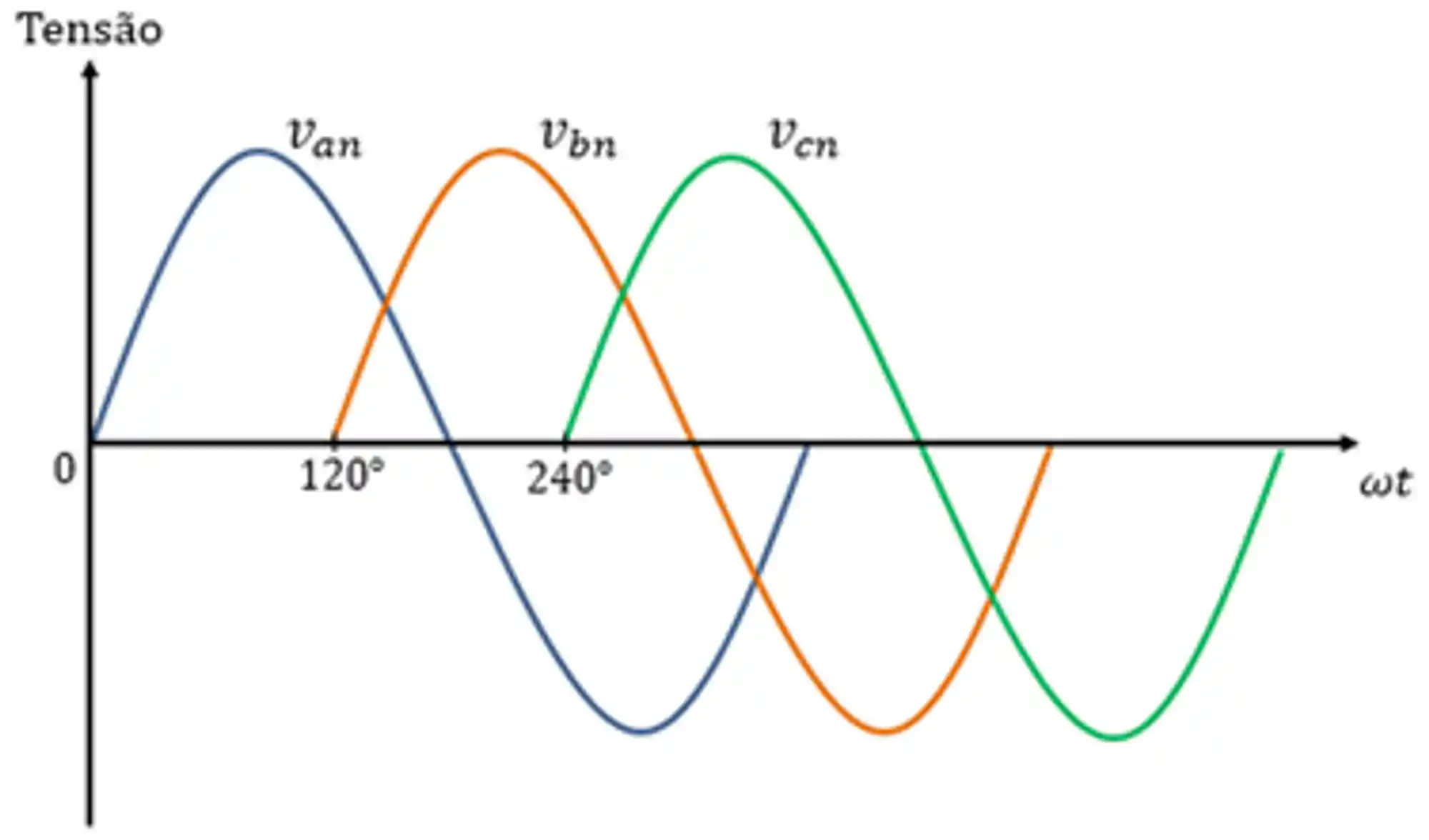
Geralmente, um sistema trifásico é formado por três fontes de tensão conectados a cargas. Tanto as cargas quanto as fontes de tensão podem ser conectadas em Estrela
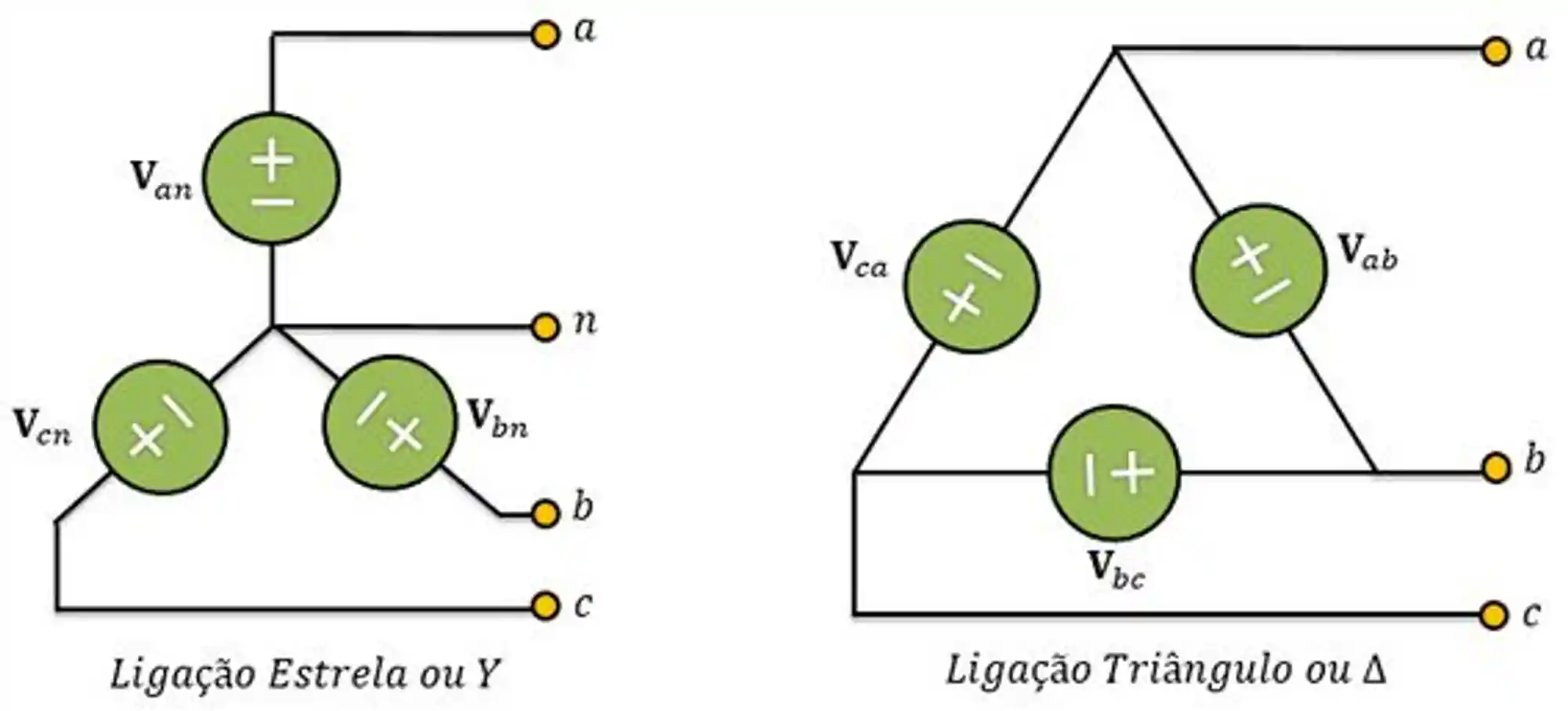
📢 Clique para ver mais:
Tensões de Fase Equilibradas
Chamamos de tensão de fase a tensão no braço da ligação, ou seja, a tensão entre uma das fases e o neutro.
Daqui para frente vamos considerar que se não for mencionado se o fasor está em RMS ou com o valor de sua amplitude, consideraremos V está em RMS, porque é o que acontece na prática.
Sequência de Fases
A sequência de fases é definida pelo sentido de rotação do gerador e podemos ter duas situações possíveis:
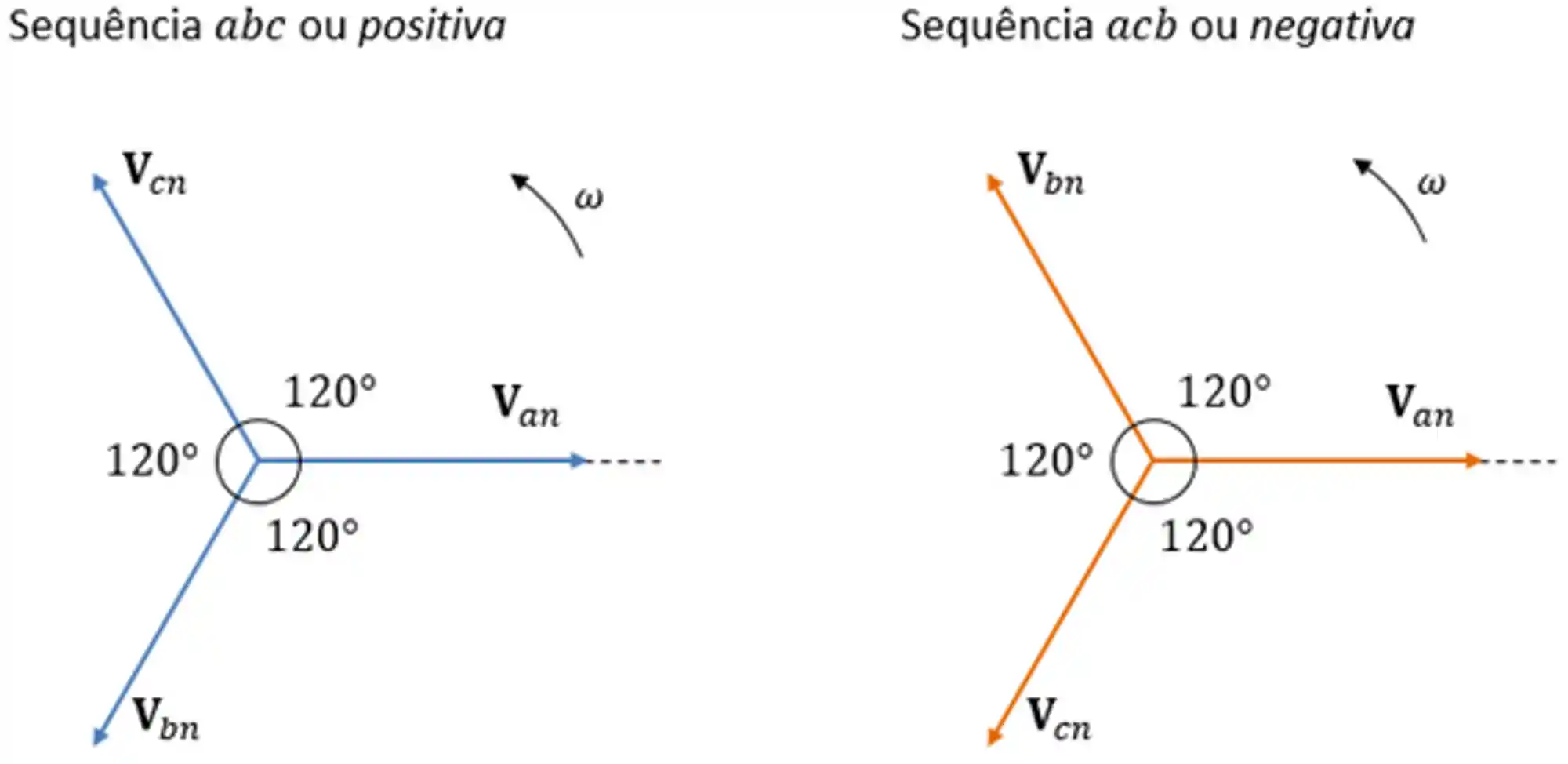
A sequência de fase é determinada pela ordem com que os fasores passam por um determinado ponto no diagrama de fase. Então, você sempre escolhe como como referência o eixo horizontal e vê qual a sequência das fases que passa por ele quando elas giram no sentido da frequência
Sequência abc
Escolhendo
Como vimos lá em cima!
Você também pode conferir esse conteúdo em vídeo:
Sequência acb
Se escolhemos a sequência anti-horária, temos:
Carga Equilibrada
Assim como as fontes de tensão em um sistema trifásicos são conectados em triângulo ou estrela, a carga também é conectada da mesma forma.
Carga Conectada em Triângulo
Podemos representar a carga conectada em triângulo da seguinte forma:
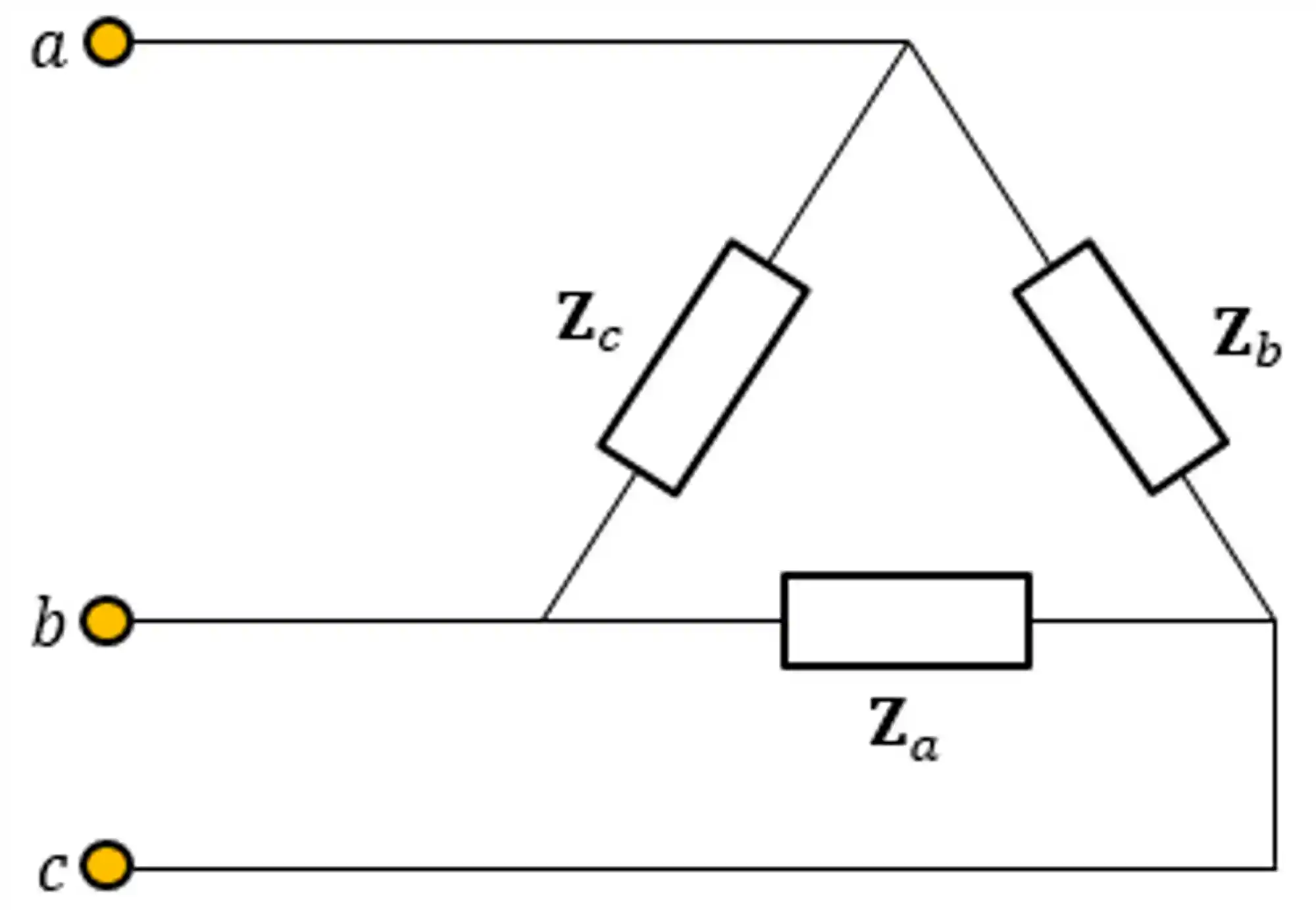
Uma carga é considerada equilibrada quando as impedâncias de cada fase são iguais em módulo e ângulo. Logo, para uma carga em estrela:
Carga Conectada em Estrela
Já a carga conectada em estrela fica assim:
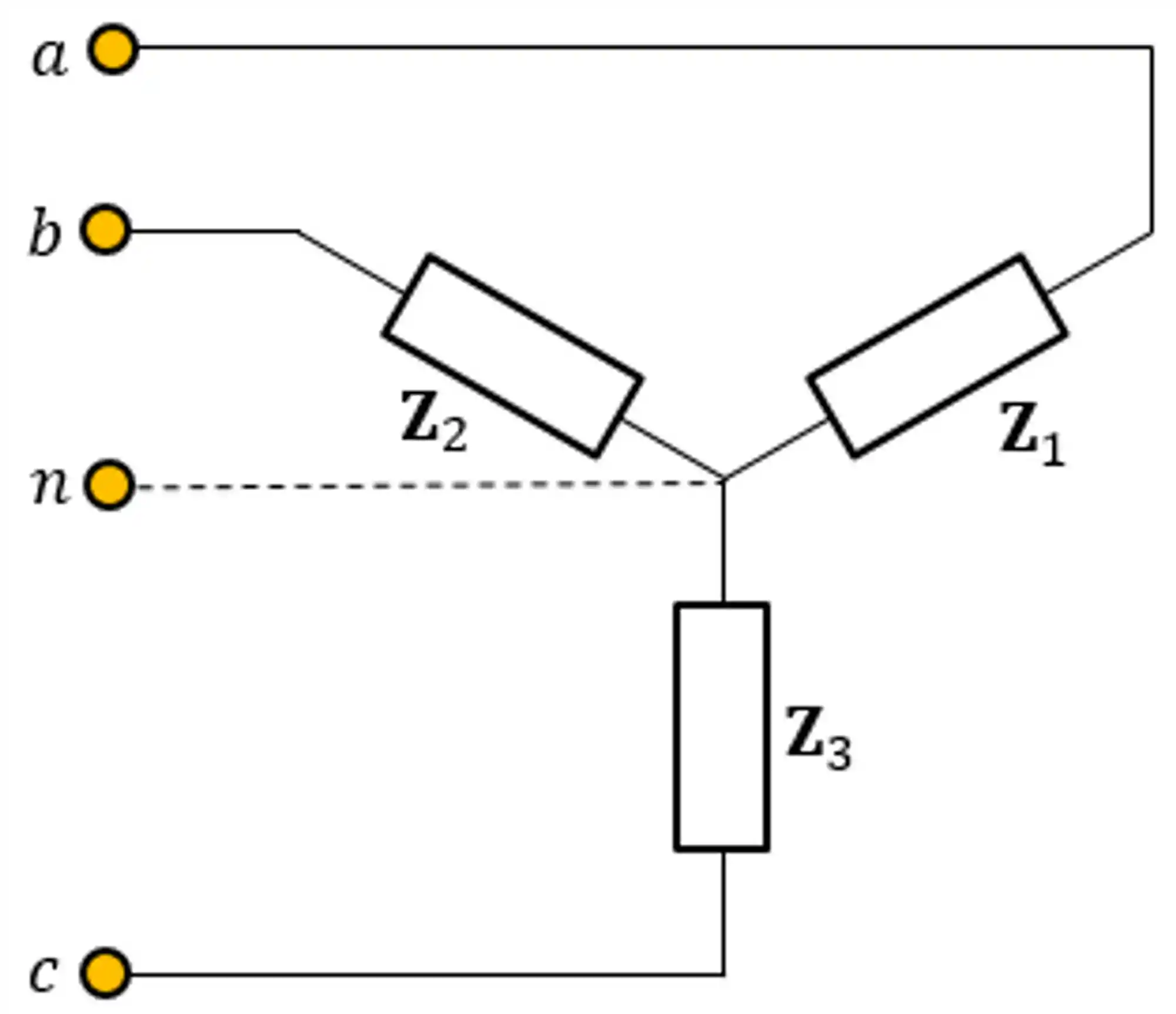
Nesse caso, para que a carga esteja em equilíbrio deveremos ter:
Lembrando que podemos transformar uma carga conectada em estrela em uma conectada em triângulo, ou vice-versa, através da relação:
Tensões de Linha e Fase
Em circuitos trifásicos temos dois tipos de tensão: a de linha
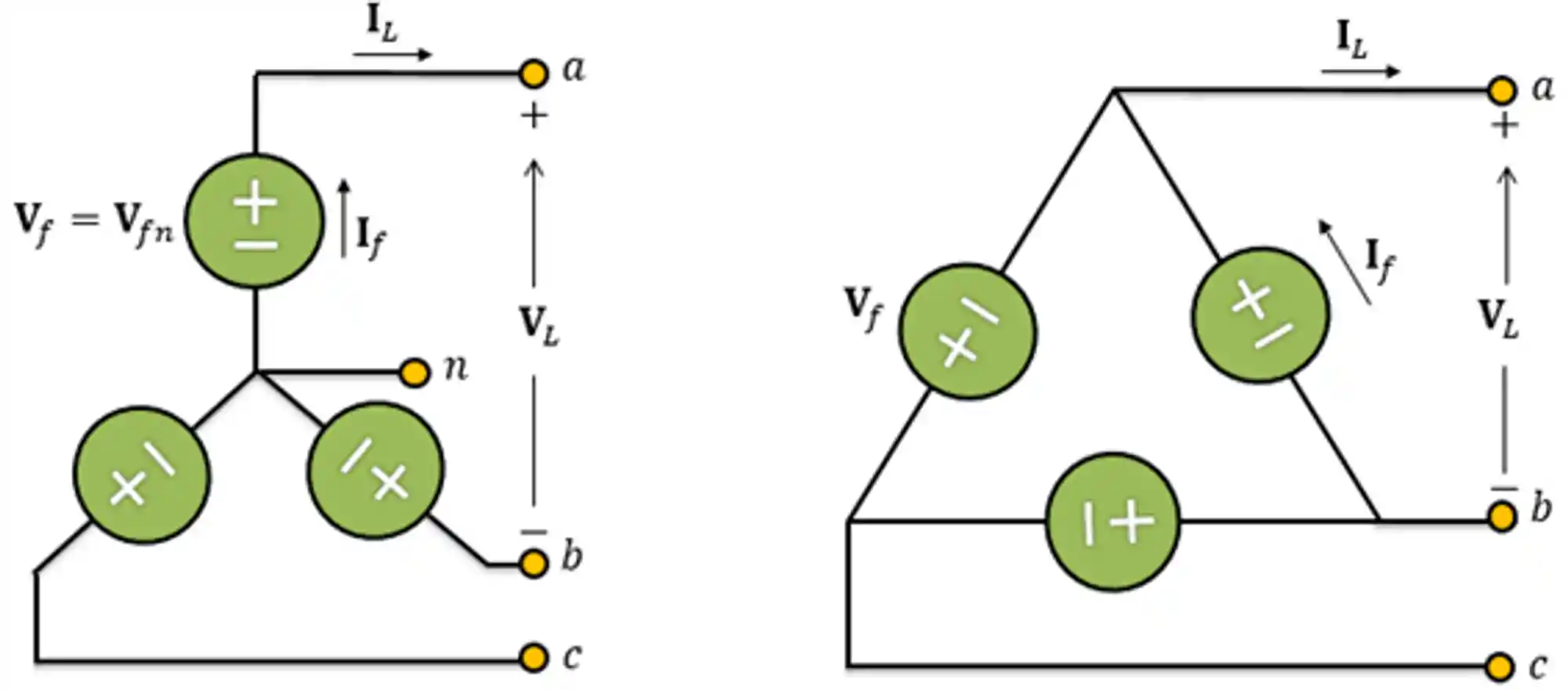
Agora vamos praticar com exercícios?!
Tensões de Fase Equilibradas
Sequência de Fases
Carga Equilibrada
Tensões de Linha e Fase
Exercícios Resolvidos
Exercício Resolvido #1
Livro Sadiku, p.484, Problema 12.2
Qual a sequência de fases de um circuito trifásico equilibrado para o qual e ? Determine .
Passo 1
O enunciado diz que o circuito é trifásico equilibrado. Então, a gente precisa lembrar de duas coisas:
- O módulo das tensões é igual
- As tensões estão defasadas entre si de 120°
Isso significa que já sabemos o módulo de , que será:
Passo 2
Agora precisamos encontrar o ângulo de Vamos analisar o que temos até agora:
A tensão de fase está a 30° positivos do eixo de referência.
A tensão de fase a 90° negativos do eixo de referência.
O ângulo de defasagem entre as tensões de fase e é de 120°.
Com essas informações montei um diagrama esperto para ficar mais fácil de entender!
Com esse diagrama já dá para ver de quanto será o ângulo de , que será de +150°. Logo:
Passo 3
Para finalizar, precisamos determinar qual a sequência de fase. Na teoria, vimos esse diagrama:
Logo, no nosso exercício, como é a fase que está a da fase , a sequência de fase é negativa ou sequência .
Resposta
Sequência
Exercício Resolvido #2
Livro Sadiku, p.484, Problema 12.1
Se em um gerador trifásico conectado em estrela equilibrado, determine as tensões de fase supondo que a sequência de fases seja:
Passo 1
A conexão estrela de um circuito trifásico é representada abaixo:
O enunciado fornece o valor da tensão de linha e diz que o circuito é equilibrado. Logo, o módulo das tensões de linha e serão iguais ao módulo da tensão de linha que foi fornecida, . Então:
Passo 2
Agora precisamos analisar para descobrir os ângulos das tensões de linha. Considerando que esteja na referência e adotando sequência como foi pedido na letra a):
Passo 3
Beleza! Estamos quase lá! Já temos módulo e ângulo de todas as tensões de linha. Só que o enunciado pede as tensões de fase. E agora?
Agora temos que lembrar da relação entre as tensões de linha e de fase em um circuito trifásico ligado em estrela:
Primeiro, vamos calcular o módulo de cada tensão de fase do circuito em estrela:
Passo 4
Agora precisamos analisar os ângulos de cada tensão de fase. Está lembrado o que modifica no ângulo quando passamos da tensão de linha para a tensão de fase na sequência ? Então... A gente tem que subtrair em cada ângulo de fase:
Prontinho!
Passo 5
Para a letra b), o que muda é que a sequência é e isso vai influenciar no ângulo das tensões. Então:
Passo 6
Da mesma forma, precisaremos calcular as tensões de fase. O módulo de cada uma delas será igual:
Passo 7
Por último, temos que analisar o ângulo das tensões de fase. Temos que tomar cuidado porque ao invés de subtrair , teremos que somar, como veremos abaixo.
Supondo que as tensões de fase sejam:
Como:
Passando para a forma polar, teremos que:
Ou seja: para a sequência , a relação entre tensão de linha e tensão de fase será:
Logo, para o nosso exercício:
Para :
Para :
Resposta
Exercício Resolvido #3
Livro Sadiku, p.484, Problema 12.3
Determine a sequência de fases de um circuito trifásico equilibrado no qual e Obtenha .
Passo 1
O enunciado diz que o circuito é trifásico equilibrado. Logo, o módulo das tensões será igual e, portanto, já temos o módulo de :
Passo 2
O próximo passo é determinar o ângulo da fase . Para ficar fácil de visualizar, fiz esse diagrama esperto com os dados que foram fornecidos no enunciado.
Lembrando que em um circuito trifásico equilibrado as tensões estão defasadas entre si de .
Logo, a tensão está a da referência, então:
Passo 3
Por último, precisamos determinar qual a sequência de fase. No diagrama do passo 2 dá para ver que quem está a da fase é a tensão . Logo, a sequência de fase é .
Da teoria tem o esquema abaixo se quiser relembrar:
Resposta
Sequência de fase
Exercício Resolvido #4
Livro Sadiku, p.484, Problema 12.4
Um sistema trifásico com sequência e alimenta uma carga conectada em estrela com Determine as correntes de linha.
Passo 1
O enunciado diz que a carga está conectada em estrela. Logo, temos a seguinte relação:
Como o enunciado fornece apenas o módulo da tensão de linha e diz que a sequência é , temos que escolher uma tensão para estar na referência, para, em seguida, calcular a tensão de fase.
Escolhendo a tensão da fase para estar na referência e lembrando que a sequência é , teremos:
Passo 2
O próximo passo é calcular as correntes. De acordo com a Lei de Ohm:
Para a fase :
Para a fase :
Para a fase :
Resposta
Exercício Resolvido #5
Livro Sadiku, p.484, Problema 12.5
Para uma carga conectada em estrela, as expressões no domínio do tempo para três tensões linha-neutro nos terminais são:
Escreva as expressões no domínio do tempo para as tensões linha-linha , e .
Passo 1
Como o enunciado pede a tensão de linha do circuito, primeiro temos que passar as tensões de fase fornecidas para o domínio da frequência:
Passo 2
Agora, vamos lembrar a relação de módulo e ângulo das tensões de linha e fase para uma carga conectada em estrela:
Logo, as tensões de linha no domínio da frequência serão:
Passo 3
Como o exercício pede as tensões de linha no domínio do tempo, teremos que passar cada uma delas:
Resposta
Exercício Resolvido #6
Livro Sadiku, p.484, Problema 17.
Uma carga conectada em triângulo equilibrada tem corrente de linha . Determine as correntes de fase , e .
Passo 1
Como a carga é um triângulo (ou delta) equilibrado, o módulo das correntes de linha será o mesmo para cada uma. Considerando sequência , teremos as seguintes correntes de linha:
Passo 2
Lembrando a relação entre corrente de linha e de fase para uma carga conectada em triângulo:
Para calcular o contrário, ou seja, a corrente de fase, vamos fazer o contrário com a corrente de linha dada:
Logo, calculando as correntes de fase:
Resposta
Exercício Resolvido #7
Livro Sadiku, p.485, Problema 12.16
Uma carga conectada em triângulo equilibrada possui uma corrente de fase .
- Determine as três correntes de linha supondo que o circuito opera na sequência de fases positiva.
- Calcule a impedância de carga se a tensão e linha for .
Passo 1
Primeiro vamos desenhar o esquema do circuito:
Além disso, pelo enunciado
Logo,
Para tirar o sinal negativo do módulo, temos que somar ao ângulo.
Passo 2
O enunciado nos disse que a sequência de fase é positiva . Logo, como o circuito é equilibrado, as correntes estão defasas de e serão:
Passo 3
Agora que a gente tem as correntes de fase vamos encontrar as correntes de linha que são pedidas na letra . Para isso, precisamos lembrar que as correntes de linha têm módulo vezes o módulo das correntes de fase, ou seja:
Além disso, as correntes de linha estão atrasadas de em relação às correntes de fase correspondentes. Logo,
Agora é só defasar de para encontrar as outras correntes de linha:
Passo 4
Sabendo que , basta aplicarmos a lei de Ohm:
Logo,
Resposta
Exercício Resolvido #8
Livro Sadiku, Problema 12.11 (adaptada)
No sistema estrela-triângulo mostrado na figura, a fonte é uma sequência positiva com e impedância por fase . Calcule a tensão de linha . Calcule também a corrente de fase e a corrente de linha .
Passo 1
Para calcular a tensão de linha, que é a tensão entre fases, por exemplo, a tensão , teremos:
Portanto, a tensão de linha sera:
Passo 2
Agora, podemos encontrar a corrente de fase. Como a nossa carga está conectada em Delta, podemos encontrar a corrente de fase fazendo:
Ou seja, a corrente que passa pela carga (que é a corrente de fase) é calculada como:
Passo 3
Para finalizar, vamos calcular a corrente de linha, essa corrente se chama assim pois ela é a corrente que passa na “linha de transmissão”, então seria a corrente por exemplo que sai da fonte em direção as cargas.
Aqui, você pode fazer o seguinte,
Primeiro vamos converter a impedância em delta para estrela (:
Agora calculamos a tensão de linha:
Agora temos uma carga equivalente conectada em estrela, e sendo assim, olhando para uma fase apenas, temos uma fonte de tensão conectada a uma carga e o neutro, ou seja, a corrente que circula por essa carga é a própria corrente de linha.
Resposta
Exercício Resolvido #9
Livro Sadiku, Problema 12.23 (adaptada)
Um sistema trifásico equilibrado com tensão de linha igual a alimenta uma carga conectada em triângulo com .
(a) Determine a corrente de linha.
Passo 1
Antes de qualquer coisa, temos que perceber que a tensão é RMS, logo temos que fazer a mudança para encontrar o valor de pico:
Logo nossa tensão de pico será:
Passo 2
Primeiro vamos calcular a corrente de fase:
Como a ligação é em delta, então as tensões de linha e de fase são iguais, ou seja:
Substituindo os valores do enunciado:
Passo 3
A corrente de linha será:
Resposta
Exercício Resolvido #10
Livro Sadiku, Problema 12.24
Uma fonte conectada em triângulo equilibrada tem tensão de fase e uma sequência de fases positiva. Se esta for conectada a uma carga em triângulo equilibrada, determine as correntes de linha e de fase. Adote como impedância de carga por fase e impedância de linha por fase .
Passo 1
Vamos converter tudo para o equivalente Y (tanto a impedância quando a fonte)
Passo 2
Vamos agora fazer o desenho do circuito:
Passo 3
Agora vamos calcular cada corrente:
Como,
Então,