Circuitos Trifásicos Desequilibrados
Produzido por Alexandre NunesTeoria
Agora que você já está fera em circuitos trifásicos equilibrados vamos ver como funcionam os desequilibrados.
Um circuito trifásico é considerado desequilibrado quando as fontes de tensão estão desequilibradas ou a carga é desequilibrada.
Fontes de Tensão Desequilibradas
As fontes são desequilibradas quando:
- A amplitude das fontes não é a mesma em todas as fases.
- As fontes não estão defasadas de entre si:
Por exemplo, na figura abaixo temos uma fonte de tensão trifásica onde seus ângulos estão defasados de e o módulo da fase é diferente dos módulos das fases e :
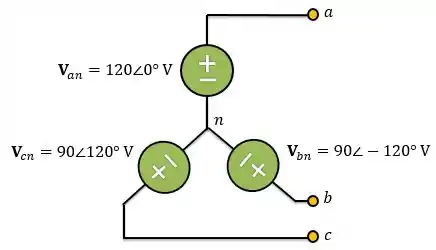
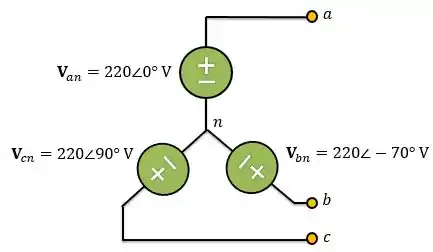
No exemplo acima, apesar dos módulos das tensões de todas as fases serem os mesmos, os seus ângulos não estão defasados em .
Então, se tivermos algum dos casos acima ou os dois ao mesmo tempo já podemos considerar o circuito trifásico desequilibrado independente das cargas.
Carga Desequilibrada
A carga trifásica é considerada desequilibrada quando as impedâncias das fases são diferentes. Por exemplo, na figura abaixo a impedância da fase é diferente da impedância da fase que é diferente da impedância da fase .
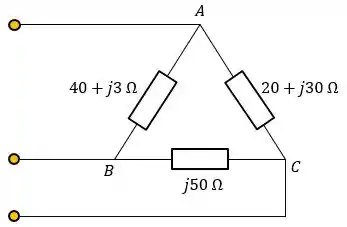
Na maioria dos circuitos desequilibrados a fonte é equilibrada e a carga trifásica é desequilibrada, como essa aí de cima.
Em circuitos desequilibrados temos que ter cuidado, porque as relações entre tensões de linha e de fase e as relações de corrente de linha e de fase não são mais válidas!

Para resolvê-los utilizamos os métodos de análise de circuitos que já conhecemos, como a análise de malha e análise nodal. Então vem comigo! Vamos fazer um exemplo.
No circuito abaixo, temos uma carga em triângulo desequilibrada alimentada por uma fonte trifásica equilibrada. Considerando e sequência positiva, vamos determinar as correntes de linha , e .
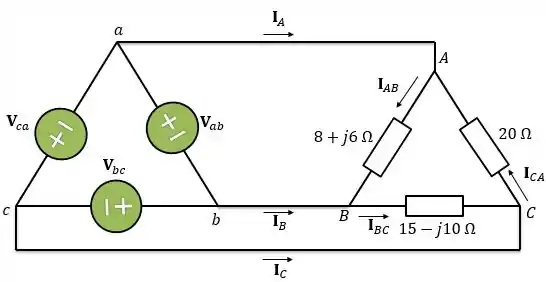
Passo 1:
O primeiro passo é determinar as correntes de fase , e . Vamos calculá-las utilizando a famosa lei de Ohm:
Além disso, o enunciado disse que a fonte é equilibrada com e que a sequência é positiva. Então,
Partiu então calcular as correntes de fase:
Passo 2:
Agora que temos as correntes de fase, vamos encontrar as correntes de linha aplicando a Lei das correntes de Kirchhoff em cada nó da carga trifásica.
Para o nó , temos:
Já para o nó :
Por fim o nó :
Pronto! Encontramos as correntes de linha do circuito. Como podemos ver elas são bem diferentes umas das outras e se multiplicarmos as correntes de fase por não encontraremos o valor correto.
Por exemplo:
Seu módulo é
Se multiplicarmos por a corrente de fase não encontraremos o mesmo valor:
Então não podemos utilizar essas relações em circuitos trifásicos desequilibrados!
Se liga na dica: se o circuito trifásico for em triângulo , como no exemplo acima, é mais fácil resolvê-lo utilizando a lei dos nós. Assim como se o circuito for em estrela é mais fácil resolvê-lo utilizando análise de malhas.
Potência
Assim como não podemos utilizar as relações entre correntes e tensões de linha e de fase, também não podemos utilizar as fórmulas de potência que conhecemos para circuitos trifásicos equilibrados em circuitos trifásicos desequilibrados.
Por exemplo, para calcular a potência complexa total absorvida pela carga, não podemos calcular a de uma fase e multiplicar por três, temos que calcular a potência de cada fase separadamente e somar depois.
No nosso exemplo seria assim:
Onde,
Então, somando a potência complexa de cada fase determinamos a potência complexa total:
Agora é fazer os exercícios para praticar!
Potência
Exercícios Resolvidos
Exercício Resolvido #1
Livro Sadiku, p.488, Problema 12.51
Considere o sistema triângulo-triângulo mostrado na figura abaixo. Adote , e .
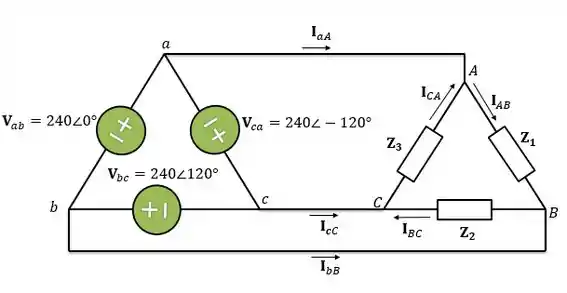
Determine as correntes de fase , e
Calcule as correntes de linha , e
Passo 1
O circuito acima é desbalanceado porque as impedâncias possuem valores diferentes. Logo, para calcularmos as correntes de fase, vamos utilizar a Lei de Ohm.
Calculando
Calculando
Calculando
Passo 2
Agora, calculando as correntes de linha, utilizaremos a Lei dos Nós.
Para o nó :
Para o nó :
Para o nó :
Resposta
Exercício Resolvido #2
Livro Sadiku, p.488, Problema 12.55
Uma fonte trifásica com tensão de linha e sequência de fase positiva tem uma carga conectada em triângulo desequilibrada, conforme indicado na figura abaixo. Determine as correntes de fase e a potência complexa total.
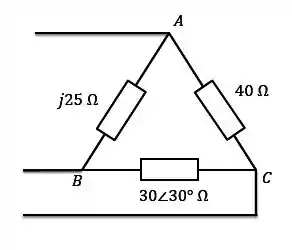
Passo 1
Primeiro, vamos determinar as tensões. Como foi dito que a sequência de fase é positiva e foi dado o valor do módulo da tensão de linha:
Passo 2
Para calcular as correntes de fase, vamos utilizar a Lei de Ohm:
Passo 3
A potência complexa em cada fase será:
Passo 4
Agora que calculamos a potência complexa em cada uma das fases, para calcularmos a potência complexa total, temos que somar cada parcela:
Resposta
Exercício Resolvido #3
Livro Sadiku, p.488, Problema 12.52
Um circuito estrela-estrela quadrifilar possui
Se as impedâncias forem
determine a corrente na linha do neutro.
Passo 1
Temos um circuito quadrifilar. Isso quer dizer que a ligação entre a fonte e a carga é feita por quatro fios, ou seja, que o neutro da fonte está conectado ao neutro da carga, como podemos ver no circuito abaixo:
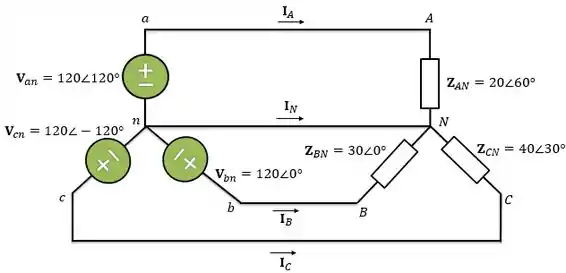
Passo 2
Queremos determinar a corrente de neutro . Para isso, vamos aplicar a lei das correntes de Kirchhoff em um dos nós:
Então, primeiro temos que calcular a corrente de linha de cada fase.
Da fase , temos:
Passo 3
Fazendo o mesmo para as outras fases, temos:
Para fase :
Para fase :
Passo 4
Substituindo pelos valores que encontramos para as correntes de cada linha, temos que a corrente de neutro será:
Resposta
Exercício Resolvido #4
Livro Sadiku, p.488, Problema 12.54
Uma fonte trifásica conectada em estrela equilibrada com alimenta uma carga trifásica conectada em estrela com impedância por fase , e . Calcule as potências de linha e a potência complexa total liberada para a carga. Suponha que os neutros estejam interligados.
Passo 1
Como nada foi dito, assumimos que a sequência da fonte trifásica é positiva, ou seja, sequência . Logo:
O circuito descrito no enunciado é esse aqui:
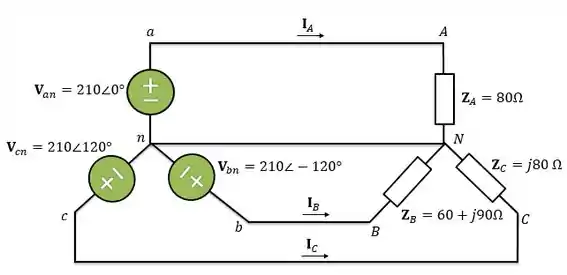
Passo 2
Para calcular as potências de linha e potência complexa total, precisaremos calcular as correntes. Logo, utilizando a Lei de Ohm:
Passo 3
Agora vamos para o cálculo das potências de linha. Primeiro temos que lembrar da fórmula:
Lembrando que na fórmula utilizamos o conjugado da corrente e, por isso, devemos trocar o sinal do ângulo dela.
Logo:
Passo 4
A potência complexa total será a soma de cada parcela calculada no passo anterior:
Resposta
Exercício Resolvido #5
UFRJ – Segunda avaliação – Professor Bruno França – Questão 1
Uma fonte trifásica com sequência , com na referência tem uma carga ligada em delta não equilibrada, conforme a figura abaixo. Determine:
As correntes de fase
As correntes de linha
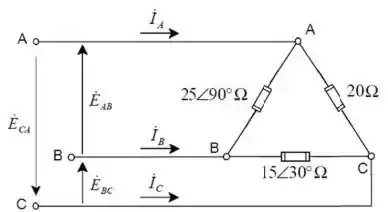
Passo 1
O enunciado diz que a sequência é . Logo, conseguimos descobrir as outras tensões:
Passo 2
Agora já podemos calcular as correntes de fase:
Passo 3
Para calcular as correntes de linha, utilizaremos a Lei dos Nós. Para isso, precisamos saber em qual sentido estão as correntes de fase em cada carga do delta.
Observando o sentido das setas, conseguimos descobrir onde é o positivo e o negativo. Como a corrente flui do positivo para o negativo, conseguimos descobrir o sentido das correntes de fase:
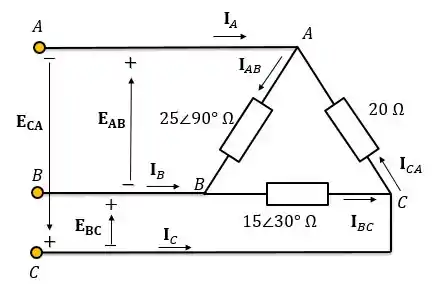
Passo 4
Finalmente, vamos calcular as correntes de linha.
Para o nó :
Para o nó :
Para o nó :
Resposta
Exercício Resolvido #6
Livro Sadiku, p.489, Problema 12.57
Determine as correntes de linha para o circuito trifásico abaixo:
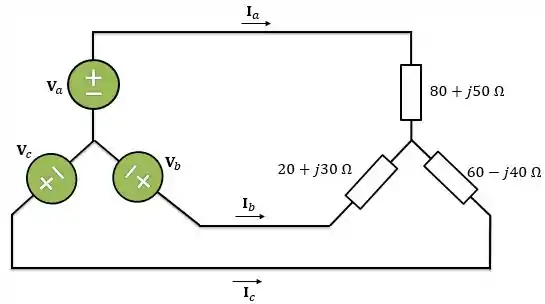
Seja
Passo 1
Para esse circuito vamos utilizar análise de malhas para determinar as correntes de linha. Para isso, vamos escolher os sentidos para as correntes de malha e :
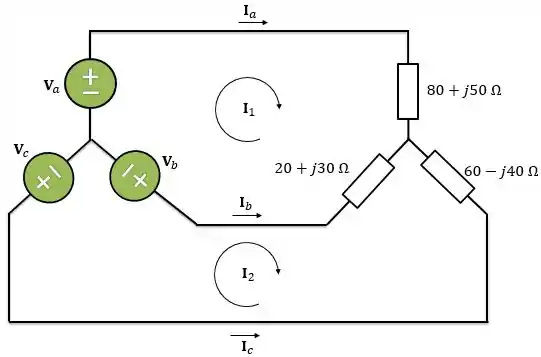
Passo 2
Aplicando a lei das tensões de Kirchhoff na malha , temos:
Passo 3
Aplicando a lei das tensões de Kirchhoff na malha , temos:
Chegamos na equação final:
Passo 4
Temos duas equações e duas incógnitas. Primeiro, vamos isolar na primeira equação:
Agora, vamos substituir na equação final encontrada no passo 3:
Passo 5
Substituindo o valor que encontramos para na equação abaixo, temos:
Passo 6
Analisando o circuito, temos que:
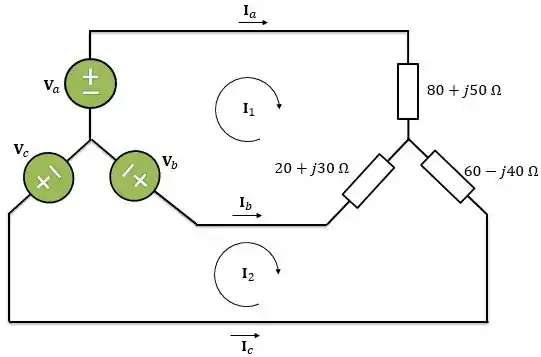
Portanto, as correntes de linha serão:
Resposta
Exercício Resolvido #7
Livro Sadiku, p.488, Problema 12.59
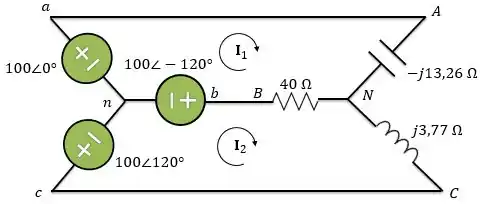
A fonte do circuito abaixo está equilibrada e apresenta uma sequência de fases positiva. Se , determine , e .
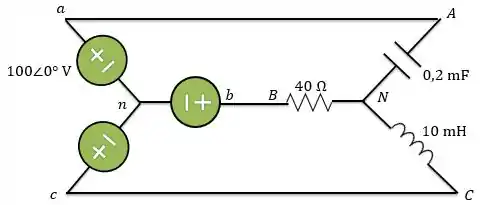
Passo 1
Primeiro, vamos determinar as impedâncias correspondentes ao capacitor e ao indutor.
Além disso, como a sequência de fase é positiva, as tensões na fonte são:
Então, temos o seguinte circuito:
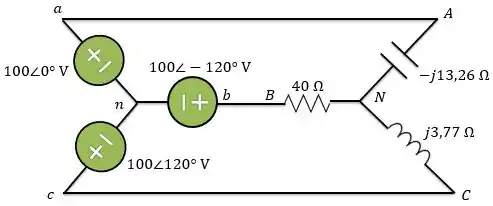
Passo 2
Para esse circuito vamos utilizar análise de malhas para determinar as correntes de linha. Para isso, vamos escolher os sentidos para as correntes de malha e :
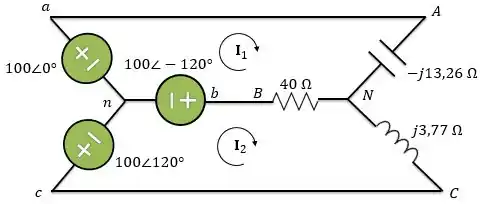
Passo 3
Aplicando a lei das tensões de Kirchhoff na malha , temos:
Passo 4
Aplicando a lei das tensões de Kirchhoff na malha , temos:
Passo 5
Temos duas equações e duas incógnitas. Primeiro, vamos isolar na primeira equação:
Agora, vamos substituir na segunda equação:
Passo 6
Substituindo o valor que encontramos para na equação abaixo, temos:
Passo 7
Aplicando a lei de Ohm podemos encontrar as tensões em cada fase na carga.
Resposta
Exercício Resolvido #8
Livro Sadiku, Problema 12.66
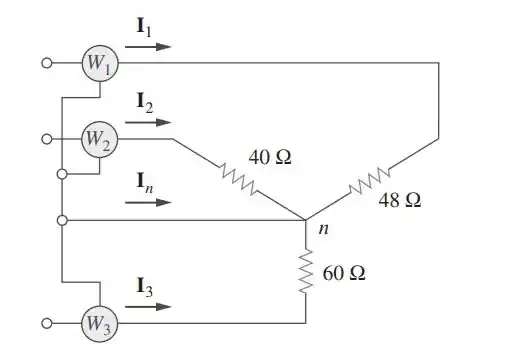
Um sistema trifásico quadrifilar operando com tensão de linha igual a é mostrado na figura. As tensões da fonte estão equilibradas. A potência absorvida pela carga resistiva conectada em estrela é medida pelo método dos três wattímetros. Calcule:
(a) A tensão para o neutro.
(b) As correntes e.
(c) As leituras dos wattímetros.
(d) A potência total absorvida pela carga
Passo 1
Na letra (a) ele quer apenas a tensão de fase que é a tensão para o neutro. Como o enunciado nos dá a tensão de linha, então:
Passo 2
Na letra (b) vamos começar assumindo que a sequência é positiva pois não foi dito nada no enunciado sobre a sequência de fase.
Vamos calcular cada corrente separadamente pois é um sistema desequilibrado por causa das diferentes resistências na carga.:
Para a corrente de neutro vamos fazer uma análise nodal e passar todas as correntes para sua forma retangular para facilitar nossa soma:
ou
Passo 3
Agora na letra C, queremos as leituras dos Wattímetros que nada mais é do que calcular as potências em cada fase:
Passo 4
Para a potência total, basta somar todas as potências calculadas no passo 3:
Resposta
(a)
(b)
(c)
(d)
Exercício Resolvido #9
Livro Sadiku, Problema 12.67
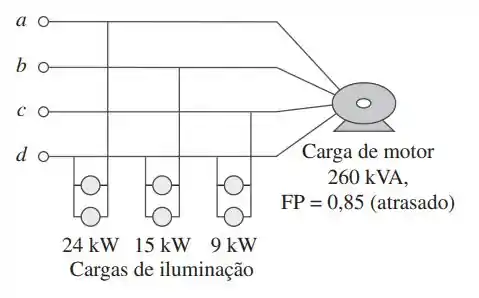
Conforme indicado na figura, uma linha trifásica quadrifilar com tensão de fase igual a e sequência de fase positiva alimenta uma carga de motor equilibrada acom . A carga do motor está conectada a três linhas principais indicadas por e. Além disso, lâmpadas incandescentes (FP unitário) são ligadas como segue: da linha para o neutro, da linha para o neutro e da linha para o neutro.
(a) se forem dispostos três wattímetros para medir a potência em cada linha, calcule a leitura de cada medidor.
(b) determine a magnitude da corrente na linha do neutro.
Passo 1
Calma lá que essa questão é gigante e parece difícil por causa desse estranho aí, mas na real é bem tranquila!
Vamos começar calculando a potência ativa do motor já que ele só nos deu a potência aparente (em kVA):
Agora com isso, podemos achar a potência por fase que precisamos para poder achar a potência total de cada fase (que é exatamente o que o wattímetro vai ler, e daí já matamos a primeira questão).
Então, cada wattímetro vai ler:
Passo 2
Para a corrente de neutro, o motor não contribui com corrente de neutro pois é equilibrado. Então vamos calcular cada corrente utilizando a Primeira Lei de Ohm:
Vamos calcular as correntes com seus respectivos ângulos (sequência de fase positiva)
Passo 3
Agora, a corrente de neutro será a soma de tudo, então, pra isso, vamos passar tudo para a forma retangular:
Resposta
(a)
(b)
Exercício Resolvido #10
Livro Sadiku, Problema 12.71
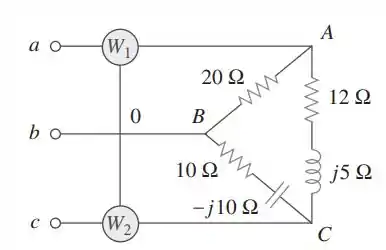
Na figura, dois wattímetros estão conectados apropriadamente à carga desequilibrada alimentada por uma fonte equilibrada tal que com sequência de fases positiva.
(a) Determine a leitura de cada wattímetro.
(b) Calcule a potência aparente total absorvida pela carga.
Passo 1
Vamos separar as tensões na sequência de fases positiva:
Daí, vamos calcular as correntes de cada fase pra poder depois calcular a potência de cada fase e consequentemente as leituras de cada wattímetro.
Vamos calcular agora cada corrente de linha (das fases A e B que é o que o enunciado pede):
Fase A:
Fase C:
Calculando as potências:
Mas, como , então,
Passo 2
Agora, para a potência total, basta somar tudo e depois achar cada potência (ativa, reativa e, então, aparente)
Resposta
(a)
(b)