Circuito RC
Teoria
Fala aí, beleza? Agora estudaremos os circuitos com resistores e capacitores e vamos querer saber o que acontece com a tensão e corrente nesses elementos ao longo do tempo.
Supondo que a gente tenha o circuito abaixo e deseja-se calcular a tensão no capacitor para todo instante de tempo a partir da chave se abrir, como resolveríamos? É isso que vamos descobrir agora!
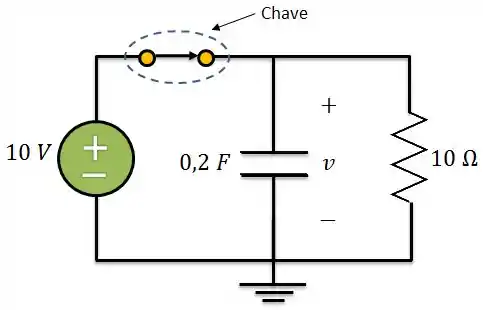
Circuito RC sem fonte
Para começar, a gente impõe que a chave esteja fechada por um longo período de tempo:
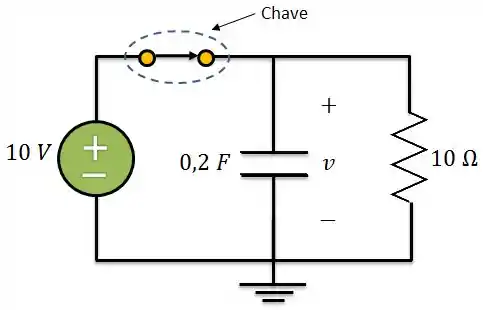
Aí, de repente a gente abre a chave:
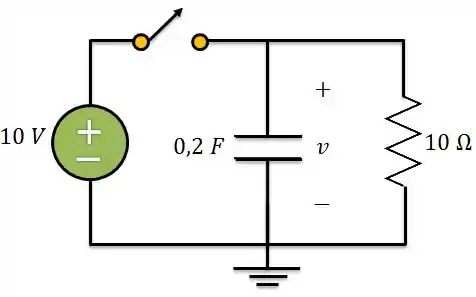
Quando a gente faz isso, o circuito passa a ser o resistor em série com o capacitor:
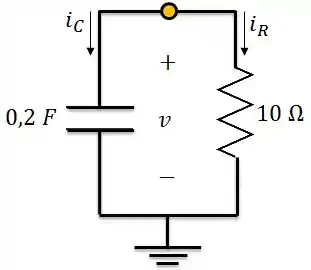
Esse circuito é chamado de circuito RC sem fonte. Agora, nossa missão é encontrar a tensão do capacitor.
Como a chave estava anteriormente fechada, o capacitor está inicialmente carregado. Então, a gente diz que no instante a tensão inicial do capacitor será a própria tensão da fonte, já que a fonte de tensão e o capacitor estão em paralelo.
Agora, vamos aplicar a LCK no nó amarelo:
A gente sabe quais são as relações de corrente no capacitor e no resistor:
Substituindo:
Essa equação é uma EDO de primeira ordem. Você lembra como resolvê-la?
Para resolver essa equação, primeiro vamos obter a equação característica:
Sabemos que a solução geral da equação é dada por:
Sendo uma constante.
Substituindo o valor de encontrado, temos:
Agora, a gente tem que encontrar o valor da constante . Lembra lá no início que a gente encontrou a tensão em ? Então, utilizaremos essa condição inicial aqui:
Logo,
Beleza! Então nossa solução final é:
Essa solução é chamada de resposta natural do circuito, pois ela só depende da energia armazena inicialmente e dos valores dos elementos do circuito.
No momento em que retiramos a fonte de tensão não há a presença de excitação externa no circuito, apenas a energia armazenada no capacitor.
Agora, vamos analisar o gráfico da resposta natural.
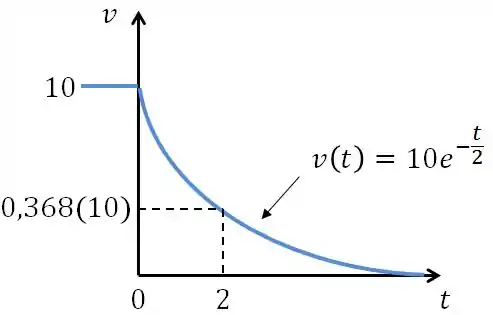
Podemos perceber no gráfico que ele parte da tensão inicial de e decresce exponencialmente até chegar a zero. Normalmente, quando queremos falar sobre a velocidade com que a essa tensão decai, falamos sobre a constante de tempo (τ) do circuito.
Por definição, a constante de tempo (τ) de um circuito é o tempo necessário para que a tensão caia 36,8% do seu valor inicial. Ou seja, para o nosso circuito, a constante de tempo seria .
Se a gente voltar nas equações, veremos que o valor de τ surgiu do produto entre a capacitância e resistência:
Logo, para esse circuito, a constante de tempo depende exclusivamente do valor dos elementos passivos.
Ufa! Muita coisa nova né?!
Vamos relembrar os passos até aqui:
- Capacitor está inicialmente carregado com uma tensão inicial:
- Aplicando LCK chegamos à EDO:
- Resolvendo a EDO:
- Encontrar a partir da condição inicial:
- Encontramos a resposta natural do circuito:
- E a constante de tempo:
Resposta ao degrau, impulso e rampa
Agora vamos estudar a resposta do circuito quando há a presença de fontes de corrente ou tensão, sem retirá-las para fazer a análise. Muitas vezes essas fontes podem ser descritas por funções singulares, como a função degrau, impulso ou rampa.
Lembrando que funções singulares são aquelas que possuem descontinuidades.
Começaremos pela função degrau unitário, que tem essa cara aqui:
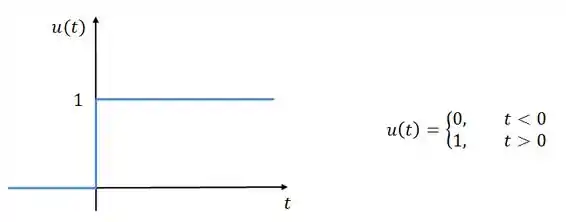
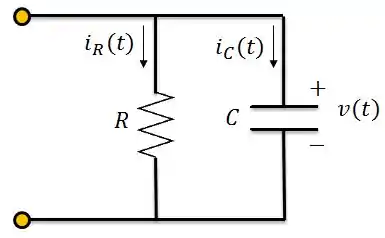
Vamos encontrar a resposta ao degrau unitário no circuito abaixo:
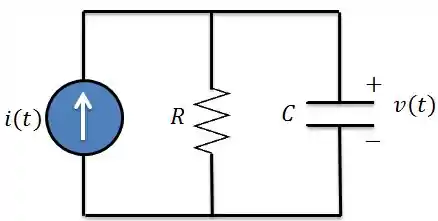
O que queremos, então, é encontrar a tensão no capacitor sendo a fonte de corrente um degrau unitário . Para isso, vamos seguir esses passos:
1º PASSO: O capacitor está inicialmente descarregado. Logo, para . Como o resistor está em paralelo com o capacitor, a tensão nos dois é a mesma.
Lembrando que a tensão no capacitor não pode variar instantaneamente, então:
Por causa disso, a corrente no instante tem que passar toda pelo capacitor, porque se passasse pelo resistor, a tensão no capacitor saltaria instantaneamente para um valor não nulo, o que não é permitido.
2º PASSO: Como a corrente inicialmente passa toda pelo capacitor, ele vai carregando e sua tensão vai aumentando. A partir desse momento, uma corrente passa a circular também pelo resistor.
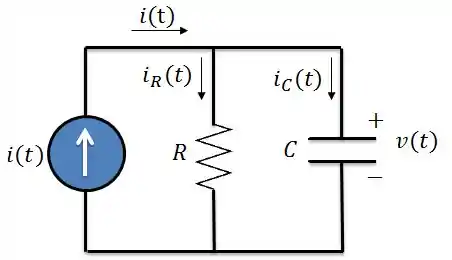
Aplicando LCK para :
Sendo
E
Como para o valor da corrente na fonte é igual a , temos:
3º PASSO: Chegamos a uma EDO não homogênea. A solução geral dessa equação é composta pela solução particular mais a solução da homogênea.
Primeiro, vamos resolver a homogênea:
Nós já resolvemos essa EDO quando estudamos o caso sem fontes e vimos que resposta é:
Agora, precisamos encontrar a solução particular.
Como é uma constante, a solução particular deve ser também uma constante:
sendo uma constante.
Substituindo, temos:
Como a derivada de uma constante é zero:
Portanto, a solução geral é:
4º PASSO: Calma, estamos quase acabando! Para terminar, precisamos encontrar o valor da constante Para isso vamos utilizar a nossa condição inicial
Substituindo:
Logo, a tensão no capacitor para qualquer instante de tempo será:
Outra maneira de escrever seria:
Graficamente a resposta ao degrau será assim:
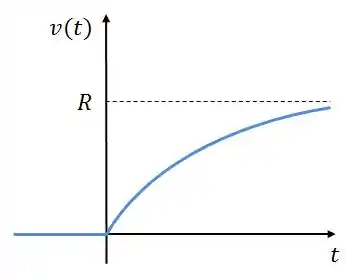
Vamos supor agora que a fonte de corrente é um impulso unitário .
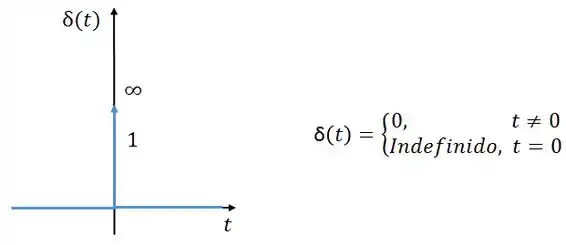
Então, quando a corrente da fonte só não é zero em Logo, para a fonte de corrente pode ser substituída por um circuito aberto, tornando o circuito igual ao caso sem fonte.
Já sabemos a solução:
No instante , um impulso de corrente no resistor causaria uma tensão infinita no capacitor, o que não é possível. Logo, o impulso de corrente deve passar pelo capacitor.
Agora se liga nesse teorema aqui: Um impulso unitário de corrente no capacitor altera instantaneamente sua tensão de zero para volts. Portanto:
Sabendo disso, já podemos calcular a constante .
Portanto, a resposta ao impulso unitário será:
Para terminar, vamos analisar quando a fonte de corrente for a rampa unitária . A gente obtém a rampa unitária integrando a função degrau unitário:
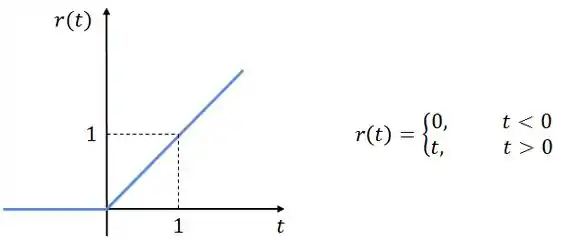
Portanto, se a gente integrar a resposta ao degrau unitário, encontraremos a resposta à rampa unitária. Logo:
Para poder assimilar tudo que estudamos até aqui, separei uns exercícios bacanas para você fixar! ;)
Resposta ao degrau, impulso e rampa
Exercícios Resolvidos
Exercício Resolvido #1
Introdução a análise de circuitos - Robert L Boylestad – Ed. 12 – Exercício 10.22
Considerando a circuito da figura, composto de valores padrão:
- Determine a constante de tempo do circuito.
- Escreva a equação matemática para a tensão depois qua chave é fechada.
- Escreva a expressão matemática para a corrente depois que a chave é fechada.
Passo 1
Para calcular a constante de tempo , vamos usar nossa conhecida fórmula:
Passo 2
Sabemos que após a chave for fechada, ocorre o carregamento do capacitor e sua tensão aumenta de acordo com a fórmula:
Passo 3
Para calcular a corrente após a chave fechar, seguimos a fórmula:
Resposta
a)
b)
c)
Exercício Resolvido #2
Livro Sadiku, p.266, Problema 7.1
No circuito mostrado na figura abaixo
- Determine os valores de R e C
- Calcule a constante de tempo
- Determine o tempo necessário para a tensão cair para a metade do seu valor inicial em
Passo 1
A primeira coisa que se pede é pra calcular o valor de R e C no circuito. Se a gente observar, R e C estão em paralelo no circuito. Então, e acordo com a lei de Ohm:
Passo 2
Agora precisamos calcular o valor de C. Na teoria de circuitos RC chegamos à seguinte relação:
Como o enunciado nos disse que a tensão é:
Então:
Passo 3
Também na teoria de circuito RC, vimos que:
Passo 4
Quando a tensão vale:
Como pede o tempo para que a tensão caia à metade, então:
Aplicando aos dois lados da equação:
Resposta
- e
Exercício Resolvido #3
Livro Sadiku, p.266, Problema 7.2
Determine a constante de tempo para o circuito RC abaixo:
Passo 1
A constante de tempo é dada pela seguinte equação:
O enunciado já fornece o valor do capacitor, que é de . Falta encontrarmos o valor da resistência.
Passo 2
A resistência será a equivalente vista pelos terminais do capacitor (terminais ). Ou seja: será o . Para calcular o , temos que curto-circuitar a fonte de tensão:
Portanto:
Passo 3
Agora já temos os dados suficientes para o cálculo da constante de tempo:
Resposta
Exercício Resolvido #4
Introdução a análise de circuitos - Robert L Boylestad – Ed. 12 – Exercício 10.25 Adaptada
Considerando o circuito RC na figura composto por valores padrão:
- Determine a constante de tempo do circuito quando a chave é colocada na posição 1.
- Determine a expressão matemática para a tensão entre os terminais do capacitor após a chave ter sido colocada na posição 1.
Passo 1
Vamos calcular a constante de tempo pedida no item a, como sabemos a fórmula é:
Passo 2
Sabemos que quando a chave é colocada na posição 1, o capacitor é carregado e sua tensão aumenta de acordo com a fórmula:
Resposta
Exercício Resolvido #5
Livro Sadiku, p.266, Problema 7.6
A chave do circuito abaixo foi fechada há um bom tempo e é aberta em . Determine para
Passo 1
O enunciado diz que a chave do circuito estava fechada há um bom tempo e que, posteriormente, foi aberta. Isso significa que o capacitor está totalmente carregado e isso faz com que ele tenha uma tensão diferente de zero em .
Passo 2
Então, vamos encontrar essa tensão em
Para isso, temos que lembrar que o capacitor em CC é um circuito aberto. Logo, podemos encontrar no circuito abaixo:
Aplicando divisor de tensão:
Em a chave está na iminência de abrir, mas ainda não abriu, e temos exatamente o circuito acima. Portanto:
Como a tensão no capacitor não pode variar instantaneamente:
Passo 3
Agora que já encontramos o valor da tensão no instante inicial, vamos encontra-la para .
Quando a chave é aberta, temos o circuito abaixo e toda a energia armazenada no capacitor vai começar a descarregar no resistor de .
Como podemos ver, o circuito acima é o circuito RC sem fonte, e sabemos que a sua resposta natural será:
Calma, foi muito rápido? Vou relembra como chegamos nessa resposta.
Vamos desenhar as correntes:
Agora, vamos aplicar a LCK no nó amarelo:
A gente sabe quais são as relações de corrente no capacitor e no resistor:
Substituindo:
Essa equação é uma EDO de primeira ordem. Você lembra como resolvê-la?
Para resolver essa equação, primeiro vamos obter a equação característica:
Sabemos que a solução geral da equação é dada por:
Sendo uma constante.
Substituindo o valor de encontrado, temos:
Viu só?
Agora, como e :
Passo 4
Para terminar, precisamos encontrar a constante . Para isso vamos utilizar a nossa condição inicial, pois em a chave acabou de se abrir:
Logo, a tensão no capacitor para será:
Resposta
Exercício Resolvido #6
Introdução a análise de circuitos - Robert L Boylestad – Ed. 12 – Exercício 10.27
Considerando o circuito RC na figura composto por valores padrão:
- Determine as expressões matemáticas para a tensão e a corrente em quando a chave é colocada na posição 1.
- Determine as expressões matemáticas para a tensão e a corrente se a chave for colocada na posição 2 a um tempo igual a cinco constantes de tempo do circuito de carga.
Passo 1
Primeiro vamos calcular a constante de tempo para a fase de carregamento:
Passo 2
Sabemos que a tensão do capacitor aumenta ao longo do tempo quando a chave está na posição 1, pois ele está sendo carregado:
Passo 3
Enquanto a tensão no capacitor aumenta, a corrente no capacitor diminui seguindo a equação:
Passo 4
Para calcular a resposta da letra b, temos que considerar que após 5 constantes de tempo, o capacitor está completamente carregado.
Logo quando a chave é colocada na posição 2, o capacitor irá descarregar a partir da tensão até 0V seguindo a equação:
Ao mesmo tempo que a corrente irá diminuir ao longo do tempo:
Passo 5
Mas temos que prestar atenção nesse detalhe aqui, como a corrente está definida no desenho no sentido para baixo:
Quando a chave estiver na posição 2, o capacitor irá descarregar e a corrente irá circular no outro sentido (para cima), logo precisamos inverter o sentido de :
Passo 6
Porém devemos perceber que a constante de tempo , pois aumentamos a resistência do circuito:
Passo 7
Substituindo os valores nas fórmulas de descarregamento:
Resposta
a)
b)
Exercício Resolvido #7
Livro Sadiku, p.270, Problema 7.40
Determine a tensão no capacitor para e no circuito abaixo:
Passo 1
Vamos começar. Enquanto a chave está na posição horizontal, formando o seguinte circuito.
Como a chave estava nessa posição há um tempo suficiente para carregar totalmente o capacitor. Ele pode ser tratado como um circuito aberto.
Passo 2
Com isso, não terá circulação de corrente. Logo, não há queda de tensão nos resistores e a tensão no capacitor será a própria tensão da fonte.
Passo 3
Em , a chave muda de posição e o circuito passa a ser assim:
Aplicando a famosa LTK no circuito:
Como,
Substituindo:
Passo 4
Chegamos a uma EDO não homogênea. A solução geral dessa equação é composta pela solução particular mais a solução da homogênea.
Primeiro, vamos resolver a homogênea:
Para resolver essa equação, primeiro vamos obter a equação característica:
Logo a solução geral da equação é dada por:
Passo 5
Agora, precisamos encontrar a solução particular.
Como é uma constante, a solução particular deve ser também uma constante:
sendo B uma constante.
Substituindo, temos:
Como a derivada de uma constante é zero:
Portanto, a solução geral é:
Passo 6
Agora, precisamos encontrar o valor da constante Para isso, sempre usamos a nossa condição inicial.
Quando a chave ainda estava na posição horizontal, mas estava na iminência de se mover, temos o instante . Nesse instante, como vimos, o capacitor está totalmente carregado.
Logo, . Lembrando que a tensão no capacitor não pode variar instantaneamente, então:
Portanto, de acordo com a nossa condição inicial, temos:
Substituindo:
Resposta
Exercício Resolvido #8
Livro Close, p.159, Problema 3.11
Determine se o circuito abaixo não contiver energia armazenada para , e se
Passo 1
O enunciado nos pede a corrente quando a tensão da fonte é o impulso unitário . Ou seja, quando tem a seguinte forma:
Passo 2
Primeiro, vamos analisar em . Como o impulso de tensão não pode ser aplicado no capacitor nem no resistor que está em paralelo com ele, porque causaria uma mudança repentina na tensão do capacitor.
Ele deve ser aplicado no primeiro resistor de , gerando um impulso de corrente:
Pronto, encontramos a corrente em .
Passo 3
Agora falta calcularmos para
Vamos distribuir a corrente como no circuito abaixo:
Aplicando a LCK, temos:
Como,
e
Substituindo:
Então, para encontrarmos para , precisamos encontrar antes para podermos substituir na equação aí de cima.
Passo 4
Agora, vamos aplicar a LTK no circuito:
Igualando as duas equações de a gente encontra:
Passo 5
Para a tensão da fonte é zero.
Vamos resolver a EDO homogênea aí de cima. Ela tem a seguinte equação característica:
Logo,
Passo 6
Precisamos encontrar a constante . Para isso, vamos analisar a tensão no capacitor no instante inicial
Lembra do impulso de corrente que falamos no início do exercício?
Então, esse impulso de corrente, ao chegar ao nó, deve circular apenas pelo capacitor, porque se alguma parcela dele passasse pelo resistor de que está em paralelo com o capacitor, causaria uma mudança repentina na tensão do capacitor.
Logo, o impulso de corrente passa pelo capacitor e de acordo com o teorema, um impulso de corrente passando pelo capacitor faz com que sua tensão instantaneamente suba para o valor do impulso multiplicado pelo inverso da capacitância.
Passo 7
Lembrando que a tensão no capacitor não pode variar instantaneamente, então:
Portanto, de acordo com a nossa condição inicial, temos:
Substituindo:
Passo 8
Agora que encontramos , podemos substituí-lo na equação abaixo para encontrarmos para
Simplificando:
Portanto:
Que também podemos escrever assim:
Resposta
Exercício Resolvido #9
Livro Close, p.160, Problema 3.16
Determine a resposta ao degrau unitário e a resposta à rampa unitária do circuito abaixo.
Passo 1
O enunciado pede para a gente determinar a tensão no capacitor para quando a fonte de corrente for um degrau unitário e para a rampa unitária . Para encontrarmos uma relação entre e , vamos fazer uma análise nodal no circuito.
Passo 2
Então, vamos fazer a análise nodal do circuito abaixo:
Aplicando LCK nos nós:
e
Escrevendo essas correntes em função das nossas tensões nodais, temos:
Substituindo esses valores nas equações nodais:
Simplificando:
Isolando na primeira equação e substituindo na segunda, obtemos:
Dando aquela ajeitada:
Como para o valor da corrente na fonte é igual a , temos:
Passo 3
Chegamos a EDO não homogênea. A solução geral dessa equação é composta pela solução particular mais a solução da homogênea.
Primeiro, vamos resolver a homogênea:
Para resolver essa equação, primeiro vamos obter a equação característica:
Logo a solução geral da equação é dada por:
Passo 4
Agora, precisamos encontrar a solução particular.
Como é uma constante, a solução particular deve ser também uma constante:
sendo B uma constante.
Substituindo, temos:
Como a derivada de uma constante é zero:
Portanto, a solução geral é:
Passo 5
Agora, precisamos encontrar o valor da constante Para isso, sempre usamos a nossa condição inicial.
O capacitor está inicialmente descarregado. Logo, para . Lembrando que a tensão no capacitor não pode variar instantaneamente, então:
Portanto, de acordo com a nossa condição inicial, temos:
Substituindo:
Que também podemos escrever assim:
Passo 6
Pronto, encontramos a resposta ao degrau unitário. Agora precisamos encontrar a resposta à rampa unitária. Sabemos que se a gente integrar a resposta ao degrau unitário, encontraremos a resposta à rampa unitária. Logo:
Que também podemos escrever assim:
Resposta
Quando
Quando
Exercício Resolvido #10
Livro Close, p.157, Problema 3.7
Determine no circuito abaixo, quando:
Passo 1
O enunciado nos pede a tensão no capacitor e a corrente quando a tensão da fonte é primeiro um degrau unitário e depois um impulso unitário . Vamos começar encontrando as equações de
Passo 2
Vamos aplicar a LCK e dividir a corrente que chega ao nó:
Passo 3
Aplicando a LTK no circuito, temos:
Como,
Substituindo:
Encontramos a EDO para a tensão no capacitor:
Passo 4
Na letra , . Ou seja, a tensão é zero até e para a tensão é constante igual a um.
Logo, para temos a seguinte EDO não homogênea:
Chegamos a uma EDO não homogênea. A solução geral dessa equação é composta pela solução particular mais a solução da homogênea.
Primeiro, vamos resolver a homogênea:
Para resolver essa equação, primeiro vamos obter a equação característica:
Logo a solução geral da equação é dada por:
sendo uma constante.
Passo 5
Agora, precisamos encontrar a solução particular.
Como é uma constante, a solução particular deve ser também uma constante:
sendo B uma constante.
Substituindo, temos:
Como a derivada de uma constante é zero:
Portanto, a solução geral é:
Passo 6
Agora, precisamos encontrar o valor da constante
O capacitor está inicialmente descarregado. Logo, para . Lembrando que a tensão no capacitor não pode variar instantaneamente, então:
Portanto, de acordo com a nossa condição inicial, temos:
Substituindo:
Logo, a tensão no capacitor para qualquer instante de tempo será:
Outra maneira de escrever seria:
Passo 7
Já encontramos para quando a fonte de tensão é um degrau unitário. Precisamos calcular agora.
A gente já tinha visto que:
Logo,
Acabamos de calcular o valor de e sabemos que .
Logo, para temos:
Logo,
Passo 8
Ufa! Terminamos a letra , vamos partir para Agora, . Já vimos que para o circuito:
Como, para o impulso unitário é zero:
Nós já resolvemos essa EDO na letra e vimos que resposta é:
Passo 9
Agora, vamos encontrar a constante . Como o impulso de tensão não pode ser aplicado no capacitor, ele deve ser aplicado no resistor , gerando um impulso de corrente de .
Como está em série com o capacitor. Esse impulso de corrente também passa pelo capacitor e de acordo com o teorema, um impulso de corrente de passando pelo capacitor faz com que sua tensão instantaneamente suba para .
Sabendo disso, já podemos calcular a constante .
Portanto, a resposta ao impulso unitário será:
Passo 10
Para terminar, precisamos encontrar para esse caso. A gente já tinha visto que:
Logo,
Acabamos de calcular o valor de e sabemos que .
Em , vimos que o impulso de tensão faz com que
Isso também ocorre com a corrente que passa pelo outro ramo:
Já para temos:
Portanto,
Que também podemos escrever assim: