Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 16.Problemas - Ex. 17

Se i s t = e - 2 t u t A no circuito mostrado na figura. Determine o valor de i 0 t .

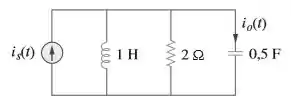
Passo 1

A primeira coisa a se fazer aqui antes de procurar a corrente é levar o circuito para o domínio de s (trabalhando as impedâncias):

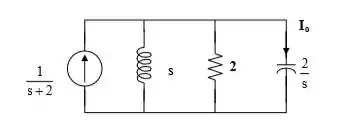
Pela Lei de Ohm, V = I ⋅ Z t ...

V = 1 s + 2 Z t

Onde Z t representa a impedância de Thévenin (Impedância equivalente vista pela fonte). A gente encontra pelo paralelo entre todas essas impedâncias:

1 Z t = 1 s + 1 2 + 1 2 s

Então...

Z t = 1 1 s + 1 2 + 1 2 s

E pela Lei de Ohm...

V = 1 s + 2 1 1 s + 1 2 + 1 2 s     →

V = 1 s + 2 1 1 s + 1 2 + s 2       →

V = 1 s + 2 1 2 + s + s 2 2 s       →

V = 1 s + 2 2 s 2 + s + s 2    

Passo 2

A corrente I 0 que atravessa a impedância capacitiva é também pela Lei de Ohm ( I = V / Z c )...

I 0 = V 2 / s = V ⋅ s 2

Logo...

I 0 = 1 s + 2 s 2 2 + s + s 2  

Para encontrar i 0 t , devemos buscara Laplace Inversa:

i 0 t = L - 1 1 s + 2 s 2 2 + s + s 2   →

E para isso, vamos separar em frações parciais:

i 0 t = L - 1 A s + 2 + B s + C 2 + s + s 2

Passo 3

Para encontrar esses valores desconhecidos, igualemos:

1 s + 2 s 2 2 + s + s 2   = A s + 2 + B s + C 2 + s + s 2   →

Colocando as frações em uma mesma fração no lado direito...

s 2 s + 2 2 + s + s 2 = A 2 + s + s 2 + B s + C s + 2 s + 2 2 + s + s 2   →

E cortando os denominadores, ficaremos com...

s 2 = A 2 + s + s 2 + B s + C s + 2   →

s 2 = 2 A + A s + A s 2 + B s 2 + 2 B s + C s + 2 C   →

s 2 = A + B s 2 + A + 2 B + C s + 2 A + 2 C →

Agora, pela igualdade de Polinômios podemos tirar o sistema:

A + B = 1

A + 2 B + C = 0

2 A + 2 C = 0

Para resolver, basta ir isolando:

A = - C

- C + B = 1 →         B = 1 + C

- C + 2 + 2 C + C = 0 →

C = - 1

Então...

A = 1       e         B = 0

Passo 4

XHOW! Então concluímos que...

i 0 t = L - 1 A s + 2 + B s + C 2 + s + s 2   →

i 0 t = L - 1 1 s + 2 - 1 2 + s + s 2   →

i 0 t = L - 1 1 s + 2 - L - 1 1 2 + s + s 2 →

A primeira Laplace já sai sem fazer nada...

i 0 t = e - 2 t - L - 1 1 2 + s + s 2 →

A segunda, a gente precisa completar quadrados:

2 + s + s 2 = s + a 2 + b 2 →

2 + s + s 2 = s 2 + 2 a s + a 2 + b 2 →

Onde a gente tira que:

2 a = 1   →         a = 1 2

E através da outra equação...

a 2 + b 2 = 2   →

b 2 = 2 - 1 4   →

b 2 = 7 4   →       b = 7 4 = 7 2

Então...

i 0 t = e - 2 t - L - 1 1 2 + s + s 2 →

i 0 t = e - 2 t - L - 1 1 s + a 2 + b 2 →

i 0 t = e - 2 t - L - 1 1 s + 1 2 2 + 7 2 2 →

Essa Laplace inversa não é o seno? NÃO! Pelo menos não ainda, falta fazer isso, veja:

i 0 t = e - 2 t - 2 7 L - 1 7 2 s + 1 2 2 + 7 2 2 →

Repare que para balancear a equação, tivemos que colocar 2 7 do lado de fora. Não se esqueça!

Então, agora sim podemos falar que...

i 0 t = e - 2 t - 2 7 e - 1 2 t sin ⁡ 7 2 t

Resposta

i 0 t = e - 2 t - 2 7 e - 1 2 t sin ⁡ 7 2 t

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use o PSpice ou MultiSim para gerar os gráficos de Bode de amplitude e de fase de V 0 no circuito da figura.
O circuito com amplificadores operacionais na figura deve sofrer uma aplicação de escala 100 na amplitude e de 10 5 em termos de frequência. Determine os valores dos elementos resultantes.
Obtenha a resposta de frequência do circuito na figura. Considere R 1 = R 2 = 100 Ω , L = 2m H . Use 1f100.000H z .
Obtenha o gráfico de amplitude da resposta V 0 do circuito da figura para o intervalo de frequências 100f1000H z .
Use o PSpice ou MultiSim para obter a resposta de frequência da figura.