Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 16.Problemas - Ex. 20
Determine para no circuito da figura.
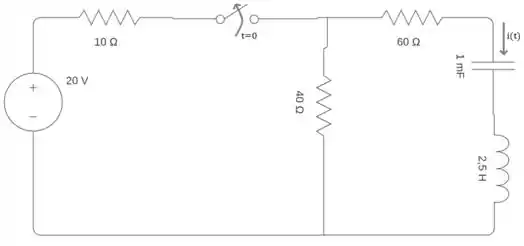
Passo 1
Vamos começar fazendo a análise antes da chave mudar de posição e depois pode ser?
Para :
Para , que é onde vamos analisar, o circuito (já no domínio , com as devidas impedâncias) é assim:
Além disso, sabemos que a corrente que passa nesse circuito em é .
Lembrando que , temos, por Lei de Kirchhoff das tensões:
Colocando em evidência:
Dividindo em cima e embaixo por :
Opa, temos um quadrado perfeito embaixo:
Passo 2
Agora vamos fazer nossas queridas frações parciais hahaha
Somando as frações com MMC:
Igualando os termos de cada lado:
Resolvendo a gente encontra isso olha:
Então:
Opa hahahaha então é só encontrar a transformada inversa de , a partir dos modelos que já conhecemos:
Sabemos que:
Portanto, teremos:
logo
Resposta
Exercícios de Livros Relacionados
Aplique os teoremas do valor inicial e do valor final a cada par de transformadas do Problema 12.43
Aplique os teoremas do valor inicial e do valor final a cada par de transformadas do Problema 12.42.
a) Calcule a área sob a função da Figura 12.12(a). b) Qual é a duração da função quando P = 0? c) Qual é o valor de f(0) quando ∈=0 ?
a) Determine a transformada de Laplace da função ilustrada na Figura P12.14. b) Determine a transformada de Laplace da derivada de primeira ordem da função ilustrada na Figura P12.14. c) Determine a t