Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 3.Problemas - Ex. 10
10. Determine no circuito da figura
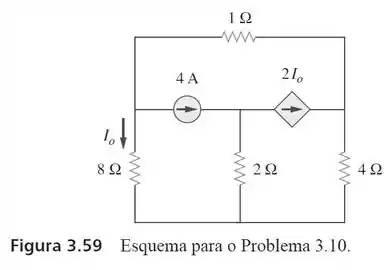
Passo 1
Bom! A primeira coisa que devemos saber antes de resolver essa questão é que a corrente elétrica irá sempre se deslocar de um ponto de maior potencial pra um de menor potencial.
E a segunda coisa que temos que fazer é de dar nomes aos bois. Essa figura tá meio vazia, né não? Precisa de um toque de classe, não concorda!?
Por isso, o que devemos fazer é dar uma embelezada nesse circuito de forma que ele possa estar mais compreensível para realizarmos a nossa análise nodal. Vamos lá...
Aqui está nossa obra de arte:
Passo 2
Nosso circuito possui nós, sendo que o nó de número está ligado à terra e portanto, possui potencial nulo.
Com isso, aplicando a para o nó , temos que:
Depois, aplicando a para o nó , temos que:
E por último, aplicando a para o nó , chegamos à:
Uma vez que a corrente sai sempre do maior para o menor potencial, vamos determinar agora as equações das correntes em relação às tensões em cada resistor:
E substituindo em seguida essas fórmulas, nas três relações que obtivemos usando o , chegamos ao seguinte sistema de equações:
Multiplicando e por e por , esse sistema pode ser simplificado em...
Peguemos agora, a equação e vamos trabalhar nela:
E depois, bora substituir essa relação encontrada, em :
Passo 3
Como o que queremos é a corrente , não precisamos das outras tensões nodais. Sabe o porquê?
Ora bolas! A corrente é dada por:
E como sabemos o valor de ...
Pronto! vale e circula em sentido oposto ao da figura do enunciado.