Resolva o Prob. 4.25 usando o método de corrente de enlace.
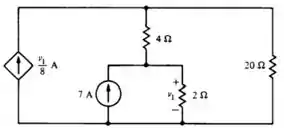
Passo 1
Falaa galerinhaa!!! Tudo tranquilo?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos pede para resolver usando o método de corrente de enlace. Puts!! Já parece difícil?? Vai ser tranquilo. Partiu??
Pessoal, infelizmente ainda não tem essa matéria no Responde Aí, porém logo logo ela ainda vai ser produzida.
Então não vamos resolver essa questão?? Mas é claro que vamos, entretanto vamos resolver pelo método da análise das malhas.
Passo 2
Então bora láa!!
Vamos começar envolvendo a fonte de corrente com o resistor de , podemos substituir pelo equivalente de Thevenin
Aplicando a Lei de Ohm, chamamos em
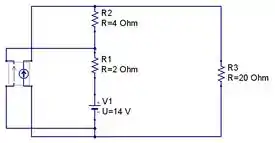
Agora envolvendo a fonte de corrente dependente por tensão com o resistor de , podemos pensar nestas superfícies como nos generalizados ou super nós.
Novamente aplicando a Lei de Ohm
Assim, o circuito resultante será
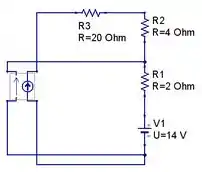
Para finalizar, vamos aplicar a LKT na malha resultante, portanto
Nossa equação (1) será
Pela tensão resultante em , chegamos na equação (2)
Sendo assim, resolvendo o sistema linear entre essas duas equações, concluímos que
Passo 3
Agora para acabarmos o exercício, vamos encontrar a potência no resistor de
Como já obtemos o valor da corrente, podemos aplicar a relação de
Substituindo os valores encontrados, chegamos em