Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 5.1 - Ex. 1

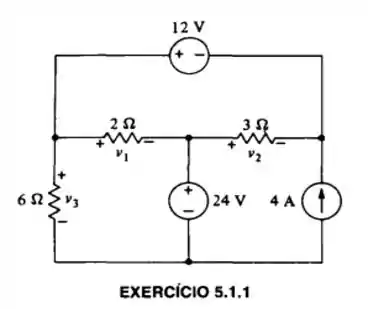
Calcule v 1 ,     v 2   e v 3 com (a) os valores das fontes como mostrado, (b) os valores das fontes divididos por 2 e (c) os valores das fontes multiplicados por 2. Note como o princípio da proporcionalidade se aplica em (b) e (c).

Passo 1

E aí, galerinha! Oia nós aqui de novo!

Simbora pro nosso primeiro exercício do capítulo 5!

Bom! O objetivo aqui é encontrar as tensões destacadas na figura do enunciado, v 1 , v 2 e v 3 .

Por isso, vamos começar dando nomes aos bois! Vamos refazer esse circuito e dar um repaginada nele...

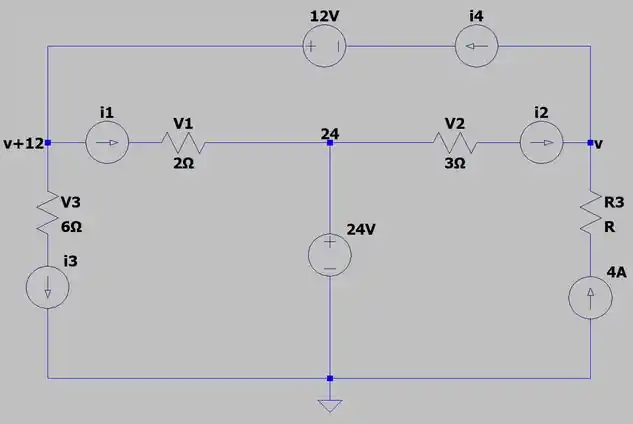
Que belezinha, né não! A gente fez isso usando um software chamado Ltspice. Depois dá uma olhada aí se tiver interesse! É bem legal!

Só que uma coisa que a gente fez diferente nesse circuito quando reproduziu ele aí no esquemático, foi supor que correntes fluem pelo circuito e também nomear os nós mais importantes desse circuito, aqueles destacados ali em v , v + 12 e 24 .

Isso aí é quanto vale a tensão nesses nós...

A gente não sabe o real sentido nem quanto valem essas correntes. Mas de acordo com a lei de kirchhoff, temos que...

i 2 + 4 = i 4

E também...

i 4 = i 1 + i 3

Logo, ficamos com...

i 2 + 4 = i 1 + i 3

Passo 2

a) Feito, a análise de corrente, vamos então recorrer à análise nodal. Temos que...

i 2 + 4 = i 1 + i 3

Substituindo...

24 - v 3 + 4 = v + 12 - 24 2 + v + 12 6

E então, rearranjando...

48 - 2 v + 24 6 = 3 v - 36 + v + 12 6

72 - 2 v = 4 v - 24

6 v = 96

v = 96 6 = 16   V

Temos que as tensões, v 1 , v 2 e v 3 ... Como podemos ver na figura, são iguais à...

v 1 = v + 12 - 24

v 1 = 16 + 12 - 24

v 1 = 4   V

v 2 = 24 - v

v 2 = 24 - 16

v 2 = 8   V

v 3 = 12 + v

v 3 = 12 + 16

v 3 = 28   V

Passo 3

b) Agora, vamo ver o que ia acontecer, se a gente trocasse aquelas duas fontes por outras duas que são metade delas, ou seja, de 12   V e 6   V e também a fonte de corrente que vai valer 2   A

Se a gente fizesse isso, a equação da análise nodal ia ficar assim...

12 - v 3 + 2 = v + 6 - 12 2 + v + 6 6

24 - 2 v + 12 6 = 3 v - 18 + v + 6 6

36 - 2 v = 4 v - 12

6 v = 48

v = 48 6 = 8   V

Percebeu!? Ao reduzirmos as fontes pela metade, v também caiu pela metade!

Substituindo, obtemos então as tensões procuradas...

v 1 = v + 6 - 12

v 1 = 8 + 6 - 12

v 1 = 2   V

v 2 = 12 - v

v 2 = 12 - 8

v 2 = 4   V

v 3 = 6 + v

v 3 = 6 + 8

v 3 = 14   V

Passo 4

(c) Por último, vamos duplicar as fontes... Fazendo isso, temos que...

48 - v 3 + 8 = v + 24 - 48 2 + v + 24 6

Isso vai nos levar à...

6 v = 192

v = 192 6 = 32   V

Pelo que iremos obter as seguintes fontes...

v 1 = v + 24 - 48

v 1 = 32 + 24 - 48

v 1 = 8   V

v 2 = 48 - v

v 2 = 48 - 32

v 2 = 16   V

v 3 = 24 + v

v 3 = 24 + 32

v 3 = 56   V

Viu só! Deu o dobro das fontes da letra (a)!

Observamos então, que ao aumentar as fontes por 2 , as fontes v 1 , v 2 e v 3 também aumentaram por 2 .

Ao dividir pela metade, as fontes também foram reduzidas à metade.

Logo, o princípio da proporcionalidade se aplica aqui!

Resposta

a)

v 1 = 4   V

v 2 = 8   V

v 3 = 28   V

b)

v 1 = 2   V

v 2 = 4   V

v 3 = 14   V

c)

v 1 = 8   V

v 2 = 16   V

v 3 = 56   V

Exercícios de Livros Relacionados

17-a) Use o método das tensões de nó para determinar vo no circuito da Figura P4.17. b) Determine a potência absorvida pela fonte dependente. c) Determine a potência total gerada pelas fontes independ
15-O circuito mostrado na Figura P4.15 é um modelo cc de um circuito de distribuição residencial. a) Use o método das tensões de nó para determinar as correntes de ramo i 1 - i 6. b) Teste sua solução
22-a) Use o método das tensões de nó para determinar vo e a potência fornecida pela fonte de corrente de 2 A no circuito da Figura P4.22. Use o nó a como o de referência. b) Repita (a) usando o nó b c
20- a) Use o método das tensões de nó para determinar vo no circuito da Figura P4.20. b) Determine a potência total dissipada no circuito. Figura P4.20
18- Use o método das tensões de nó para calcular a potência gerada pela fonte de tensão dependente no circuito da Figura P4.18.Figura P4.18