Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 10.Problemas - Ex. 23

10.23. Calcule os valores i e v em regime permanente.

Passo 1

Fala pessoal, belezinha?

Primeiramente vamos recordar aqui do circuito da nossa questão.

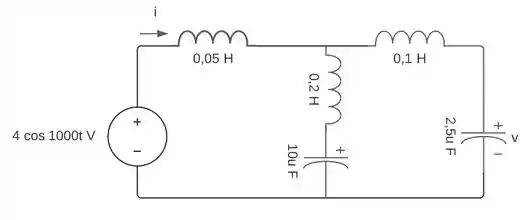
Vamos agora, calcular a resistência equivalente do circuito:

R = 100 j - 400 j = - 300 j

R ' = 2 00 j - 1 00 j 1 00 j

R ' ' = R R ' = ( - 3 00 j ) ( 1 00 j ) - 300 j + 100 j = 150 j

Z = 50 j + R ' ' = 5 0 j + 150 j = 200 j

Z = 200 ∠ 90 °

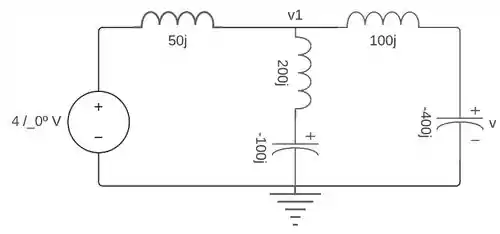
Passo 2

Agora, é possível, calcular a corrente em regime permanente i :

I = V Z = 4 ∠ 0 ° 200 ∠ 9 0 ° = 0,02 ∠ - 9 0 ° = 20 cos ⁡ 1 00 0 t - 90 ° m A

I = 20 sen ⁡ ( 1000 t - 90 ° ) m A

Passo 3

Agora, é possível, calcular a corrente em regime permanente v :

V 1 = 4 ∠ 0 °   .     150 j 200 j = 3 ∠ 0 °

V = 3 ∠ 0 °   .   - 40 0 j - 3 00 j = 4 ∠ 0 ° = 4 cos ⁡ 1000 t   V

Resposta

I = 20 sen ⁡ ( 1000 t - 90 ° ) m A

V = 4 cos ⁡ 1000 t   V

Exercícios de Livros Relacionados

Usando análise nodal, o valor de V 0 no circuito da Figura 10.45 é: - 24V b) - 8V c) 8 Vd) 24V
No circuito da Figura 10.46, a corrente i(t) é: 10 cos ⁡ tA b) 10 s e ntA c) 5 cos ⁡ tA d) 5s e ntA e) 4.472 cos ⁡ t - 63.43 ° A
O valor da corrente I 0 no capacitor da Figura 10.44 é: 4 ∠ 0 °A b) 2.4 ∠ - 90 °A c) 0.6 ∠ 0 ° Ad) - 1A
Determine i no circuito da Figura 10.50.
Usando a Figura 10.51, elabore um problema para ajudar outros estudantes a entender melhor a análise nodal.