Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 10.Questões para revisão - Ex. 4
No circuito da Figura 10.46, a corrente i(t) é:
- b) c)
d) e)
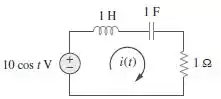
Passo 1
Vamos lá! A questão nos pede para encontrar a corrente, podemos fazer por análise de malha. Primeiro passo a se fazer é ver se todos os componentes estão no domínio da frequência. Note que,
Para o indutor:
Para o capacitor:
Passo 2
Note que,
Portanto
Resposta
Item a)
Exercícios de Livros Relacionados
Use o método das correntes de malha para determinar as correntes de ramo Ia, Ib, Ic e Id no circuito da Figura P9.62.
a) A tensão da fonte no circuito da Figura P9.40 é vg = 40 cos 1.000t V. Determine os valores de L em que i g fica em fase com vg quando o circuito estiver em regime permanente. b) Para os valores de
A frequência da fonte de tensão no circuito na Figura P9.38 é ajustada até que vg fique em fase com i g. Qual é o valor de v em radianos por segundo? b) Se i g = 60 cos vt mA (onde v é a frequência de
O fasor corrente Ib, no circuito da Figura P9.36, é 25 ∠0 º º mA.. a) Determine Ia, Ic e Ig. b) Se v = 1.500 rad/s, determine as expressões para i a(t), i c (t) e i g(t).
Use o método das tensões de nó para determinar a expressão de regime permanente para i o no circuito visto na Figura P9.56, se i g = 5 cos 2.500t A e vg = 20 cos (2.500t + 90º) V.