Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 15.Problemas - Ex. 22
Mostre que, no caso geral, a função de rede na figura do Prob. 15.1 é dada por
Desta forma. por comparação com e (15.25), mostre que o circuito é um filtro passa-faixa com frequencia de ressonăncia , largura da faixa e indice de mérito . Mostre também que o ganho do filtro. definido como seu valor de pico da amplitude, é dado, neste caso, por .
Passo 1
E aí gurizada tudo belezinha? O enunciado pede que a gente mostre também que o ganho do filtro. definido como seu valor de pico da amplitude, é dado, neste caso, por .
Vamos começar representando o circuito 😊
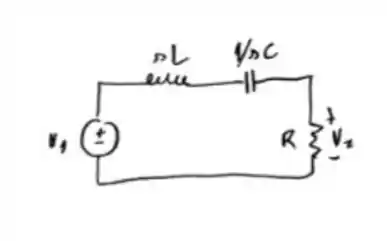
Passo 2
Formato:
Largura da faixa
Resposta
Exercícios de Livros Relacionados
Aplique análise fasorial para calcular o seguinte: v = 110 sen 20 t + 30 ° + 220 cos 20 t - 90 °V i = 30 cos 5 t + 60 ° - 20s e n 5 t + 60 °A
Usando fasores, determine i ( t ) nas seguintes equações: 2 d i d t + 3 i t = 4 cos ( 2 t - 45 ° ) 10 ∫ id t + d i d t + 6 i t = 5 cos ( 5 t + 22 ° )
Um circuito R L C em paralelo possui a equação nodal a seguir: d v d t + 50 v + 100 ∫ vd t = 100 cos ( 377 t - 10 ° )V Determine v ( t ) usando o método fasorial. Supondo que o valor da integral em
Um circuito R L C série tem R = 80Ω , L = 240m H e C = 5m F . Se a tensão de entrada for v t = 10 cos 2 t determine a corrente que flui através do circuito.
Determine a corrente que flui através de um resistor de 8Ω conectado a uma fonte de tensão v S = 110 cos ( 377 t )V .