Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 4.Problemas - Ex. 13
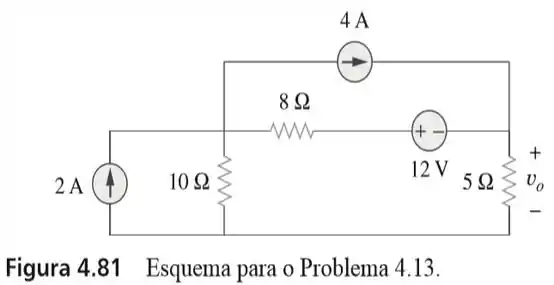
13. Use superposição para determinar no circuito da figura
Passo 1
Olha só! No circuito da figura do enunciado, há a presença de duas fontes independentes; uma fonte de tensão de e duas fontes de corrente de e , respectivamente.
Logo, usando superposição, temos que a tensão é dada pela soma das contribuições de tensão das três fontes individualmente. No caso, chamaremos de a contribuição da fonte de corrente de , de a contribuição da fonte de corrente de e de a contribuição da fonte de tensão de .
Passo 2
Primeiro, vamos determinar . Para isso, vamos retirar a fonte de tensão substituindo por um curto-circuito e substituir a fonte de corrente de por um circuito aberto.
De modo que nosso circuito passa a ter a seguinte cara:
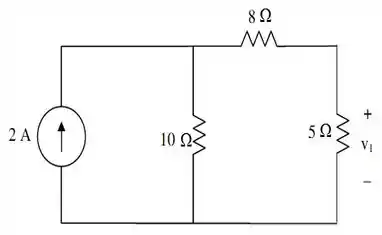
Olha só! A tensão é dada pelo produto da resistência de por uma corrente “tal” que passar por esse resistor. E essa corrente, que chamaremos de , pode ser obtida através da divisão de corrente por...
A tensão , portanto, é igual a:
Passo 3
Em seguida, vamos determinar . Para isso, vamos substituir a fonte de tensão por um curto circuito e substituir a fonte de corrente de por um circuito aberto, deixando apenas a fonte de corrente de presente.
E o circuito fica desse jeito aqui:
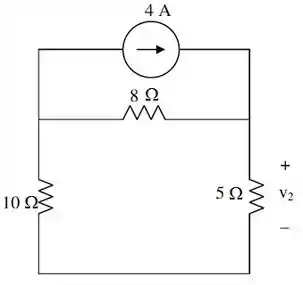
Esse caso é análogo ao anterior. A tensão é dada pelo produto da resistência de por uma corrente “tal” que passa por esse resistor. E essa corrente, que chamaremos de , pode ser obtida através da divisão de corrente por...
A tensão , portanto, é igual a:
Passo 4
Por último, vamos determinar . Para isso, vamos substituir as duas fontes de corrente por um circuito aberto, deixando apenas a fonte de tensão presente.
De modo que o circuito fica com a seguinte cara:
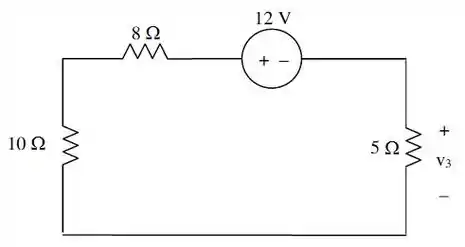
E nesse caso, a tensão pode ser determinada facilmente por divisão de tensão...
O sinal negativo advém do fato, de que ao percorrer o circuito no sentido horário, que é o sentido padrão para análise de malhas, ao passar pela fonte de tensão há uma queda de tensão. Continuando com o cálculo...
Já temos tudo o que precisamos!
Passo 5
Pra finalizar, basta somar , e e encontraremos ...
E voilà! Resposta encontrada!