57- Obtenha os circuitos equivalentes de Thévenin e de Norton nos terminais para o circuito da Figura .
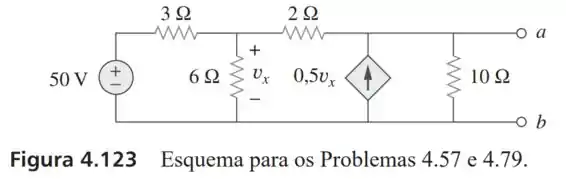
Passo 1
Não aterrando nenhum dos terminais nós inutilizamos a fonte independente de mas não a fonte dependente de , então teremos que colocar uma fonte de tensão (pois já temos uma fonte de corrente) de nos terminais e para que possamos encontrar a resistência de Norton (ou Thevénin) desse circuito ai.
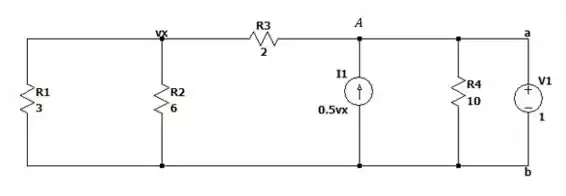
Os resistores de e de estão concectados nos mesmos pontos então elas estão em paralelo e elas nos dão uma resistência equivalente igual a:
Dessa forma nós teremos o seguinte circuito.
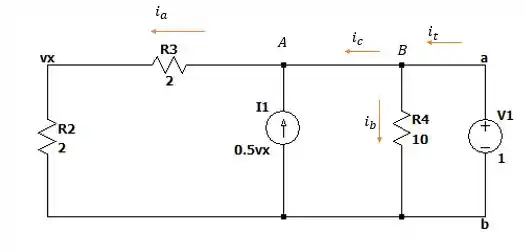
Por estar em pararelo com a fonte e não termos nenhuma resistência em série nós podemos dizer que o nó tem tensão de assim como o nó . Mas por ter uma resistência em série não podemos dizer isso de .
E justamente por terem a mesma tensão em e podemos dizer também que , já que a corrente só existe quando há diferença de tensão.
Logo pela soma das correntes no nó podemos dizer que:
Dessa forma podemos calcular pelas diferença de tensão entre o nó e , da seguinte forma:
Dessa forma temos correntes iguais a:
Pois pela soma das correntes em temos :
Só que como pela igualdade de tensão, então
Então a resitência de Norton será igual a:
Pois são as tensões e correntes geradas pela fonte que colocamos entre e .
Passo 2
Agora vamos fechar os contatos e e aterrarmos o terminal para calcularmos a corrente de Norton nesse circuito. Note que fechando esse contato nenhuma corrente passará pela resistência de pois todas as fontes estarão a esquerda dessa linha então a corrente prefirá passar toda pela linha sem a resistência. De forma que teremos o seguinte circuito.

Fazendo a somatória das tensões na malha mais a esquerda teremos:
E na malha do centro.
Dessa forma:
Então o valor de valerá:
E com isso o valor de será pela diferença de tensão:
Passo 3
Agora vamos encontrar o valor de fazendo a igualdade das correntes que entram e que saem do nó e que nos dá:
Ou seja:
Como temos a corrente de Norton e a resitência de Norton nós podemos encontrar a tensão de Thévenin fazendo: