Enunciado
Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 4.Problemas - Ex. 16
16-
Use o método das tensões de nó para determinar a potência total dissipada no circuito da Figura P4.16.
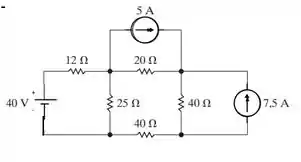
Figura P4.16
Passo 1
Então, vamos enfrentar essa fera... brincadeira rsrs. Essa questão é suave na nave, basta que a gente pense um pouquinho, vamos nessa?!
a) A partir do uso do nosso parceiro, o método das tensões de nó, temos:
Passo 2
Resolvendo temos:
v1 = −10 V;
v2 = 132 V;
v3 = −84 V;
Achando a corrente na fonte de 40V:
i40V = −10 + 40 12 = 2.5 A
A partir de então, achamos as potencias dos elementos do circuito:
p5A = 5(v1 − v2) = 5(−10 − 132) = −710W (fornece)
p7.5A = (−84 − 132)*(7.5) = −1620W (fornece)
p40V = −(40)*(2.5) = −100W (fornece)
Passo 3
Continuando com as potências...
p12Ω = (2.5)2 (12) = 75W
Passo 4
∑pdissipada = 75 + 4 + 1008.2 + 176.4 + 1166.4 = 2430W
∑pfornecida = 710 + 1620 + 100 = 2430W
A potencia total é
Resposta
2430 W.