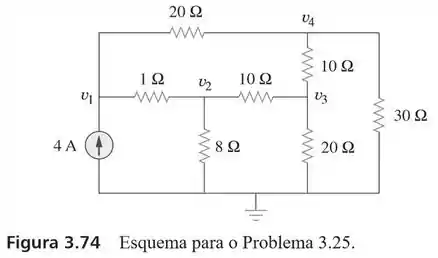
25. Use a análise nodal juntamente com o Matlab para determinar as tensões nos nós da Figura

Primeiramente, vamos escolher os sentidos das correntes e nomear as tensões de cada nó para aplicarmos a :

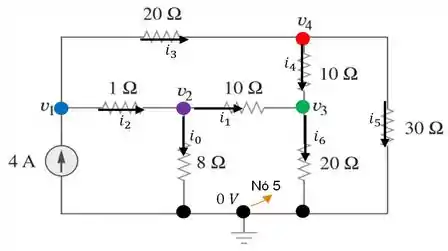
Com isso, aplicando a para o nó , temos que:

E depois, aplicando a para o nó , chegamos à:

E agora, a para o nó :

E por último, a para o nó :

Nesse , vamos determinar agora as equações das correntes em relação às tensões nodais:

E substituindo em seguida essas correntes, nas quatro relações que obtivemos do , chegamos ao seguinte sistema de equações:

Agora, bora dar uma simplificada nesse sistema:

E vamos tratar de resolver esse sistema com quatro equações e quatro incógnitas, né? Vai ser complicado, mas vamos conseguir.

Para fazer isso, vamos ter que usar uma ferramenta comum em Álgebra Linear, o escalonamento pelo método de .

A eliminação de Gauss, ou método de escalonamento, é um algoritmo para se resolver sistemas de equações lineares Este método consiste em aplicar sucessivas operações elementares num sistema linear, para o transformar num sistema de mais fácil resolução, que apresenta exatamente as mesmas soluções que o original.

Uma matriz retangular, que é o nosso caso está na sua forma escalonada ou na forma de escada por linhas quando satisfaz as seguintes condições:

Todas as linhas não-nulas estão acima de qualquer linha composta só de zeros.

O pivô de cada linha está numa coluna à direita do pivô da linha acima.

Todos os elementos de uma coluna abaixo de um pivô são zero.

Bem! Vamos pro que interessa! Esse sistema de quatro equações e quatro incógnitas do , pode ser escrito como:

Tudo que temos que fazer então, é simplicar isso aí. Para isso, vamos recorrer ao escalonamento da seguinte matriz!

Essa é a chamada matriz estendida! Se você reparar bem, no lado esquerdo dela temos os coeficientes que acompanham as incógnitas (tensões nodais) e no lado direito, o resultado de cada equação.

O que nós queremos é simplificar ao máximo essa última matriz aí, de forma que satisfaça as condições que escrevemos no . Para fazer essa simplificação, vamos manipular o sistema através de determinadas operações elementares, transformando a matriz estendida do sistema de forma a deixa-la o mais triangular possível (chamada de matriz escalonada do sistema).

Naturalmente estas operações elementares devem preservar a solução do sistema e consistem em:

multiplicação de um linha por uma constante não nula

substituição de uma linha por ela mesma somada a um múltiplo de outra linha.

permutação de duas linhas.

Chamaremos de linha e de coluna. é a linha e é coluna , por exemplo:

Vamos lá!

Pronto! Viu só como essa ferramenta foi útil! O sistema de quatro equações e quatro incógnitas de antes, vai ficar assim:

Agora ficou tudo mais fácil! Peguemos a equação :

E agora, a equação , uma vez que já sabemos o valor de :

Depois, a equação , onde já sabemos o valor de e :

Por último, a equação , dado que já sabemos o valor de , e :

Obtemos nossas respostas!

Viu só! Nem precisamos de !

Mas caso tenha alguma curiosidade! Aqui está o jeito pra resolver esse problema no ...

Escrevendo o sistema linear do na forma matricial, temos que:

Tudo que precisamos fazer então, é usar no Matlab a seguinte relação:

Onde:

No , a matriz vai ficar assim:

E fica desse jeito:

E com isso, obtemos a seguinte resposta:

Que é a mesma coisa que conseguimos em nossos cálculos!

Viu só! Acertamos em cheio!