Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 3.Problemas - Ex. 19
19. Use a análise nodal para determinar , e no circuito da figura .
Passo 1
No circuito acima, os nós já estão identificados. O nó inferior está ligado ao terra com um potencial nulo.
E com isso vamos dar início a nossa linha de pensamento.
Passo 2
Primeiramente, vamos escolher os sentidos das correntes e nomear as tensões de cada nó para aplicarmos a :
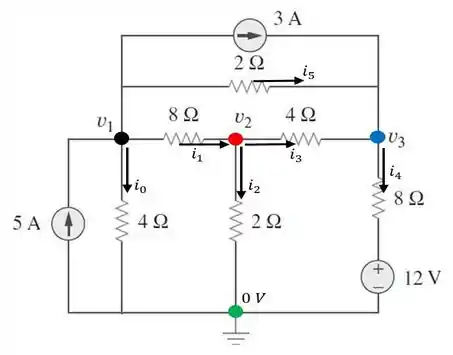
Com isso, aplicando a para o nó , temos que:
E depois, aplicando a para o nó , chegamos à:
E por último a para o nó :
Passo 3
Nesse , vamos determinar agora as equações das correntes em relação às tensões nodais:
E substituindo em seguida essas correntes, nas duas relações que obtivemos do , chegamos ao seguinte sistema de equações:
Passo 4
Agora, bora dar uma simplificada nesse sistema:
De modo a ficarmos com:
Passo 5
Xii rapaz! Isso aí tá complicado de resolver!
Por isso vamos usar uma ferramenta comum em Álgebra Linear, o escalonamento. Bem! Esse sistema de três equações e três incógnitas, pode ser escrito como:
Tudo que temos que fazer então, é simplicar isso aí. Para isso, vamos recorrer ao escalonamento da seguinte matriz!
Chamaremos de linha e de coluna. é a linha e é coluna , por exemplo:
Vamos lá!
Pronto! Viu só como essa ferramenta foi útil! O sistema de três equações e três incógnitas de antes, vai ficar assim:
Pegando a equação :
E agora, a equação :
E por último, a equação :
Obtemos nossas respostas!