27-

a) Use o método das tensões de nó para determinar as correntes de ramo i 1, i 2 e i 3 no circuito da Figura P4.27.

b) Verifique sua solução para i 1, i 2 e i 3, mostrando que a potência dissipada no circuito é igual à potência gerada.

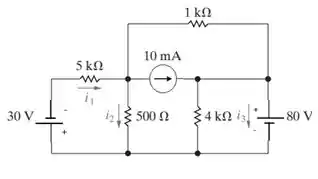
Figura P4.27

Resolvendo,

va + 30 + 10va + 5va − 400 + 50 = 0 logo,

16va = 320

va = 20 V

Calculando as correntes:

i1 =

= 0

Logo

i3 = 0,01 – 0,02 – 0,06 = −0,07 = −70 mA

b)

p30V = (30)*(−0,01) = −0,3 W

p10mA = (20 − 80)*(0,01) = −0,6 W

p80V = (80)*(−0,07) = −5,6 W

p5k = (−0,01)2 (5000) = 0,5 W

p500Ω = (0,04)2 *(500) = 0,8 W

p1k = (80 − 20)2/(1000) = 3,6 W

p4k = (80)2/(4000) = 1,6 W

∑pconsumida = 0,5 + 0,8 + 3,6 + 1,6 = 6,5W

∑pfornecida = 0,3 + 0,6 + 5,6 = 6,5 W (verificado)