Enunciado
Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 4.Problemas - Ex. 25
25-
a) Use o método das tensões de nó para determinar a potência dissipada no resistor de 2 V no circuito da Figura P4.25.
b) Determine a potência fornecida pela fonte de 230 V.
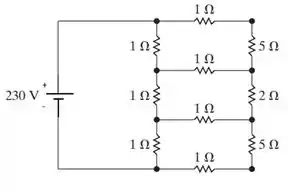
Figura P4.25
Passo 1
Falaaaaa meu querido, vamos brincar mais um pouco?? Partiuuu!!
a) Basicamente a gente já começa usando o método das tensões de nó:
= 0 Simplificando
Simplificando,
Simplificando, −12v2 + 0v3 + 20v4 − 6v5 = 460
Simplificando, 0v2 − 12v3 − 6v4 + 20v5 = 0
Passo 2
Resolvendo, temos:
v2 = 150 V;
v3 = 80 V;
v4 = 140 V;
v5 = 90 V
p2Ω = = 1250W
Passo 3
b) Para obter potência fornecida pela fonte de 230 V, fazemos o seguinte:
i230V
p230V = (230)*(95) = 21850W
Passo 4
Verificando:
∑Pconsumida = (80)2 *(1) + (70)2 * (1) + (80)2 * (1) + (15)2 * (6) + (10)2 * (1) +(10)2 * (1) + (25)2 * (2) + (15)2 * (6) = 21850W
Resposta
a) p2Ω = 1250W
b) p230V = 21850W