Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 3.Problemas - Ex. 24
24. Use a análise nodal e o Matlab para determinar no circuito da Figura
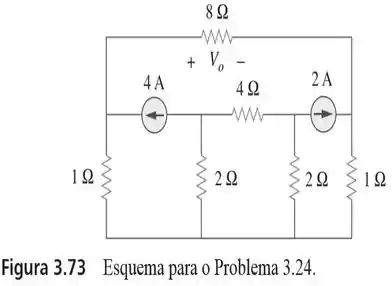
Passo 1
No circuito acima, temos cinco nós. O nó inferior vai estar ligado à terra, com um potencial nulo.
E com isso vamos dar início a nossa linha de pensamento.
Passo 2
Primeiramente, vamos escolher os sentidos das correntes e nomear as tensões de cada nó para aplicarmos a :
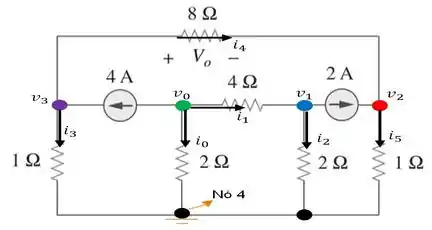
Com isso, aplicando a para o nó , temos que:
E depois, aplicando a para o nó , chegamos à:
E agora, a para o nó :
E por último, a para o nó :
Passo 3
Nesse , vamos determinar agora as equações das correntes em relação às tensões nodais:
E substituindo em seguida essas correntes, nas quatro relações que obtivemos do , chegamos ao seguinte sistema de equações:
Passo 4
Agora, bora dar uma simplificada nesse sistema:
Passo 5
E vamos tratar de resolver esse sistema com quatro equações, né? Vai ser complicado, mas vamos conseguir.
Peguemos as equações e :
E bora multiplicar por e depois somar com a :
Assim, obtemos :
E para obter , bora pegar a equação :
Passo 6
Depois, vamos pegar as equações e :
E bora multiplicar por e depois somar com a :
Assim, obtemos :
E para obter , bora pegar a equação :
Obtidas essas tensões nodais, temos tudo o que precisamos. Sabe o porquê? A tensão é dada, ao olhar o nosso circuito, por:
Viu só! Nem precisamos de !
Passo 7
Mas caso tenha alguma curiosidade! Aqui está o jeito pra resolver esse problema no ...
Vamos escrever o sistema linear do na forma matricial! Bem! Esse sistema de quatro equações e quatro incógnitas, pode ser escrito como:
Tudo que temos que fazer então, é usar no Matlab a seguinte relação:
Onde:
No , a matriz vai ficar assim:
E fica desse jeito:
E com isso, obtemos a seguinte resposta:
Que é a mesma coisa que conseguimos em nossos cálculos!
Finalmente, obtemos que a tensão é dada, ao olhar o nosso circuito, por:
Viu só! Acertamos em cheio!