Enunciado
Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 4.Problemas - Ex. 30
30-
Use o método das tensões de nó para determinar a potência fornecida pela fonte de tensão de 20 V no circuito da Figura P4.30.
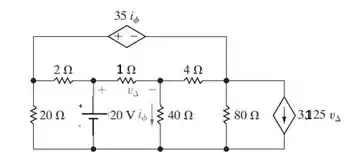
Figura P4.30
Passo 1
Falaaaa bb, vamos dá o gás e terminar essa rapidão??!!
Basicamente a gente utiliza o método das tensões de nó e encontramos as equações nodais, show!!!
Passo 2
Encontrando as equações de restrição:
v∆ = 20 − v2
v1 − 35iφ = v3
iφ = v2/40
Resolvendo, temos:
v1 = −20.25 V;
v2 = 10 V;
v3 = −29 V
Passo 3
Sabendo que é a corrente fornecida pela fonte de 20 V, temos:
Resposta
A potência fornecida pela fonte de tensão de 20 V é .
Exercícios de Livros Relacionados
A figura do Ex. 6.2 . 2 e as figuras (a) e (b) mostradas aqui sāo exemplos de um gráfico de rede escada. Existe um teorema que estabelece que o número de árvores num gráfico de escada de n ramos é o n
Calcule v no Prob. 6.8 usando os métodos da teoria de gráficos, se o elemento x é uma fonte de 4V com o terminal positivo na parte superior, y é uma fonte de 2V com o terminal positivo na parte de bai
Todas as resistências são de 1 Ω , o elemento w também é um resistor de 1 Ω , os elementos x e y sāo fontes de corrente independentes de 1 A fluindo para cima e o elemento z é uma fonte independente d
Encontre. se for possível, a árvore que contenha todas as fontes de tensão e os ramos cujas tensões controlam fontes dependentes, mas mio contenham fontes de corrente ou ramos cujas correntes controla
12-Use o método das tensões de nó para determinar v1 e v2 no circuito da Figura P4.12.