Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 2.Problemas - Ex. 33
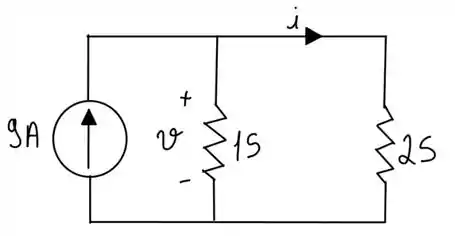
33. Obtenha v e i no circuito da Figura 2.97
Passo 1
Vamos associar os resistores para facilitar nossas contas. Primeiro os resistores de com o de , como o exercício nos fornece as condutâncias vamos trabalhar com elas.
Para associar duas condutâncias em série usamos a seguinte formula:
Ou também:
Perceba que é a mesma coisa da resistência em paralelo.
Aplicando os valores na formula:
Passo 2
Agora essa condutância que encontramos está em paralelo com a de
E para associar condutâncias em paralelo é só soma-las:
Passo 3
E então temos, novamente, que associar as condutâncias em série:
Então o circuito ficou dessa forma:
Agora podemos usar a fórmula para o divisor de corrente com as condutâncias:
Como a corrente que passa pela consutância de é de a queda de tensão provocada por ela é de:
Logo, se a diferença de potencial entre os terminais da condutância de é igual a , a diferença de potencial entre os terminais da condutância de também será de , pois, são estão conectados nos mesmos nós. Então: