Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 3.Problemas - Ex. 43
43. Use a análise de malhas para determinar e no circuito da figura
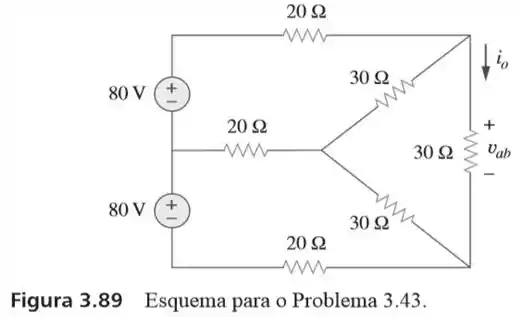
Passo 1
Bom! Se estamos trabalhando com análise de malhas, então temos que nomear as correntes de malha de cada uma das três malhas do nosso circuito.
Bora fazer então, o esboço do circuito com as correntes de malha já indicadas...
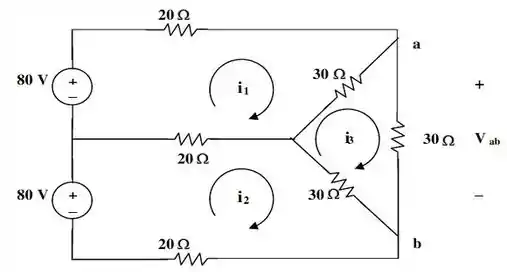
E agora, vamos finalmente aplicar a análise de malhas pra esse nosso circuito.
Bora primeiro percorrer a malha . Olha só! O objetivo aqui, é determinar as tensões nessa malha. E para isso, consideremos as quedas de tensão como positivo e as elevações de tensão como negativo. A soma disso tudo tem que dar zero...
Passo 2
Em seguida, bora percorrer a malha . Repetindo o mesmo procedimento do ...
Passo 3
E percorrendo por fim, a malha ; chegamos que:
Passo 4
Obtemos assim, o seguinte sistema de equações:
Bom! Essa questão aqui, a gente não vai precisar do , ou outro software não. Reparou que o termo é comum a todas essas equações.
Vamos então somar as equações e e depois as equações e . Chegamos, desse modo, a um sistema de duas equações:
Multipliquemos então, a primeira equação por e depois bora com a segunda equação:
Já o valor de é dado por:
Para encontrar , basta usar...
A corrente é igual à corrente de malha ... Sendo assim:
E a tensão é dada pelo produto da resistência de pela corrente...