Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 6.Problemas - Ex. 18
Resolva o Prob. 4.29 usando métodos da teoria de gráficos.
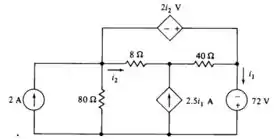
Passo 1
Falaa galerinhaa!!! Tudo tranquilo?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos pede para resolver usando o método da teoria dos gráficos. Puts!! Já parece difícil?? Vai ser tranquilo. Partiu??
Pessoal, infelizmente ainda não tem essa matéria no Responde Aí, porém logo logo ela ainda vai ser produzida.
Então não vamos resolver essa questão?? Mas é claro que vamos, entretanto vamos resolver pelo método da análise de malha.
Passo 2
Então bora láa!!
Com a análise de malha nosso circuito ficará o seguinte
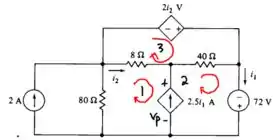
Ok, agora vamos começar utilizando o equivalente de Thevenin na malha sem numeração. Responde Aí!! Lembra como faz?? Não?!
Bora lá
Então vamos substituir por uma fonte de tensão em série com o resistor
Agora vamos aplicar a análise de malhas no circuito
Somando as equações (1),(2) e (3), chegamos em
Pela equação (4)
…(5)
Continuando pela equação (4)
Pela LKC
…(6)
Substituindo (6) em (5)
Passo 3
Agora vamos para o último passo!!
Substituindo os dados obtidos na soma entre (1) e (2)
Como
Pronto!!