Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 10.Problemas - Ex. 53
53. Use o conceito de transformação de fontes para determinar no circuito da figura .
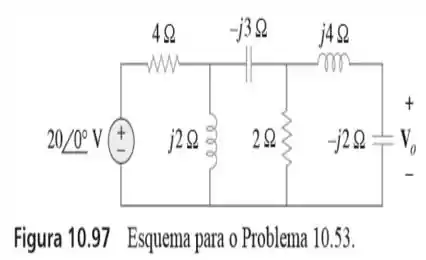
Passo 1
A primeira coisa que temos que fazer é pensar num jeito de tornar esse circuito mais fácil pra gente trabalhar.
Por isso, vamos usar a transformação de fontes nessa parte aqui do circuito...
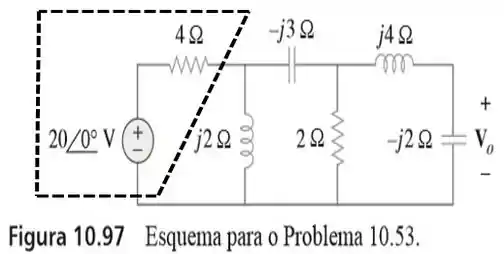
Essa associação em série entre uma fonte de tensão e uma resistência, pode ser transformada em uma associação em paralelo entre a mesma resistência e uma fonte de corrente , que é dada por:
Passo 2
Nosso circuito então, fica assim:
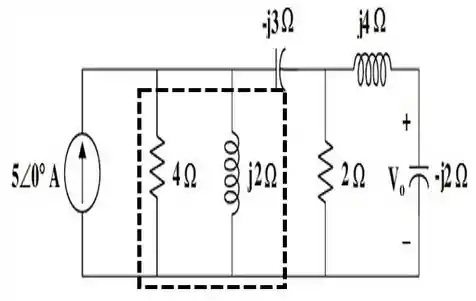
E desse jeito, bora calcular a impedância equivalente, para a parte do circuito envolta pelo retângulo pontilhado. Ela é dada por:
Multiplicando essa impedância pela fonte de corrente do anterior, obtemos o valor da tensão representada pela associação em paralelo entre a impedância e a fonte de corrente.
Passando para a forma retangular:
Passo 3
Na prática,o que fizemos foi usar novamente uma transformação de fonte. De uma associação em paralelo entre uma fonte de corrente e uma impedância, ficaremos com uma associação em série entre uma fonte de tensão e a mesma impedância.
Desse jeito aqui:
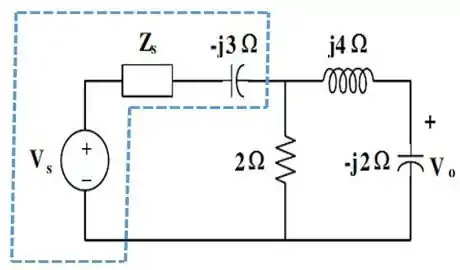
E novamente vamos usar a transformação de fontes. Temos que transformação essa parte envolta pela região pontilhada azul numa associação em paralelo entre a impedância dessa parte e uma fonte de corrente, que chamaremos de .
é dada por:
Substituindo os valores, que já foram obtidos no , chegamos ao seguinte resultado...
Passo 4
Diante disso, nosso circuito passa a ter a seguinte cara:
Essa impedância , é na verdade, igual a .
Pra simplificar ainda mais nosso circuito, bora obter a impedância equivalente, que chamaremos de , pra essa região retangular preta tracejada. Ela é dada por:
Multiplicando essa impedância pela fonte de corrente do anterior, obtemos o valor da tensão representada pela associação em paralelo entre a impedância e a fonte de corrente.
Passo 5
E com isso, chegamos então, ao seguinte circuito simplificado:
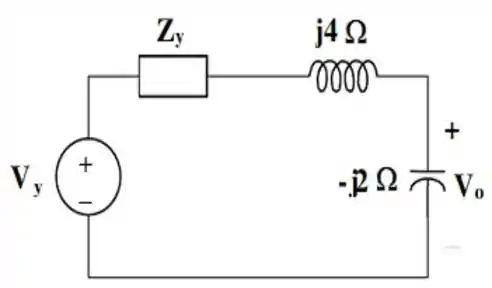
Para obter o valor de , que é o nosso principal objetivo, bora usar a divisão de tensão. Por esse método, temos que é dada por:
Substituindo os valores numéricos pertinentes:
Passando para a forma retangular:
E voilà! Resposta obtida: