Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 4.Problemas - Ex. 66
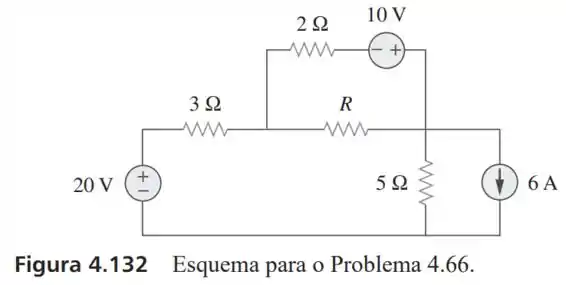
66- Determine a potência máxima que pode ser liberada para o resistor no circuito da Figura .
Passo 1
Na seção vemos que a potência máxima em se dará quando for igual a resistência equivalente de Thevenin para os terminais onde ela se situa e ela terá valor igual a:
Vamos retirar a resistência e ficar com os terminais da seguinte forma:
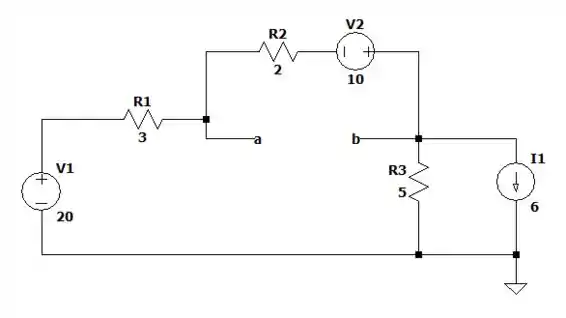
Aí agora vamos desconectar as fontes independentes para conseguirmos descobrir a resistência de Thévenin do circuito.
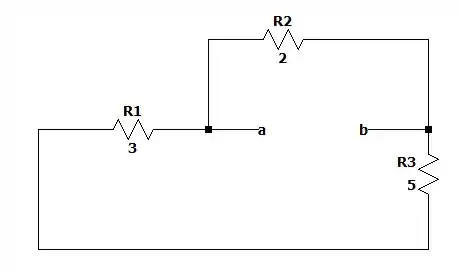
Desenhando esse circuito de outra forma temos a mesma coisa que isso aqui.
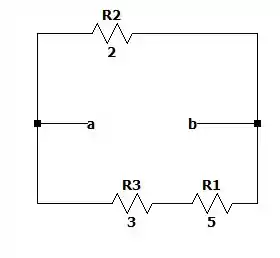
Onde podemos ver que temos duas resistências em paralelo, uma de e outra de , o que nos dá uma resistência de Thevenin igual a:
Passo 2
Agora vamos descobrir a tensão de Thevenin mas antes vamos facilitar nossa vida e transformar a fonte de em uma fonte de tensão. Da seguinte forma:
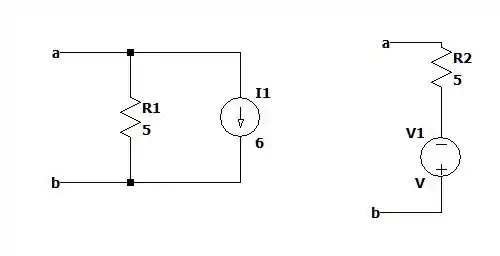
Onde valerá:
Substituindo isso no circuito teremos:
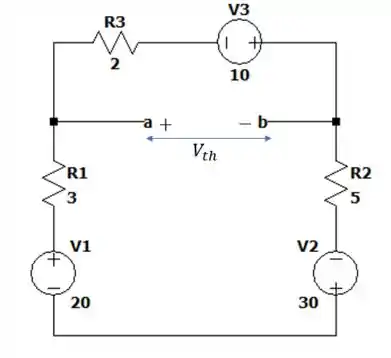
Somando as duas tensões e as duas resistências na malha de baixo nós vamos ter:
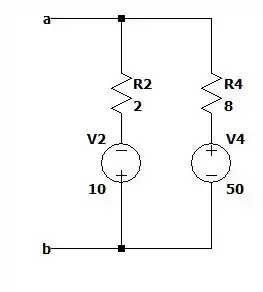
Passo 3
Uma forma simples de resolver isso é convertermos essas duas fontes de tensão em duas fontes de corrente de forma que vamos ter a seguinte representação.
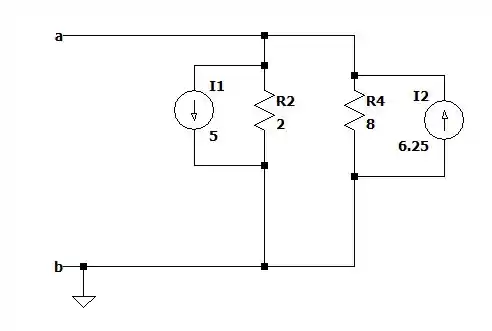
Somando as duas fontes e fazendo a resistência equivalente de e de que estão em paralelo, nós iremos obter.
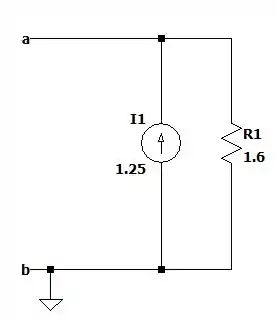
O que nos dá a resistência de Norton, então essa é a corrente de Norton. Logo a tensão de Thevenin será:
Então a potência máxima será igual a: