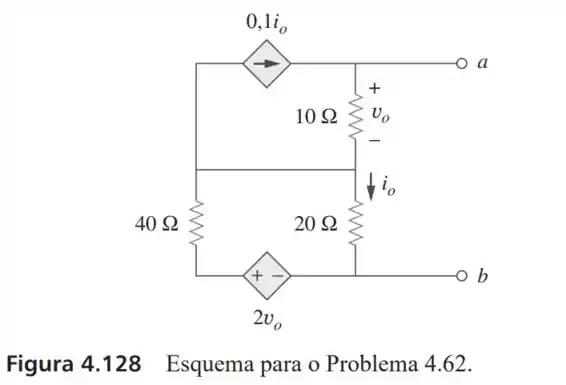
62- Determine o equivalente de Thévenin do circuito da Figura .
Passo 1
Falaee, tranquilinho?? O enunciado nos deu o seguinte circuito:
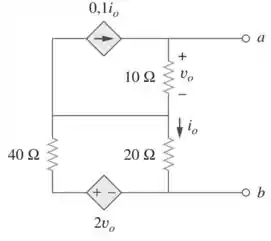
Queremos encontrar o equivalente de Thévenin desse circuito.
Bom... Se aterrarmos e conectarmos com não encontraremos nenhuma corrente de Norton sobre esses terminais, assim como não encontraremos tensão de Thévenin, isso se dá pela falta de tensões independentes pois se dizermos que e tem a mesma tensão nós iremos zerar e o que nos faz não ter essas duas fontes. Logo:
Assim, precisamos encontrar a resistência de Thévenin!!
Passo 2
Pela falta de fontes dependentes vamos colocar uma fonte de tensão de entre e da seguinte forma:
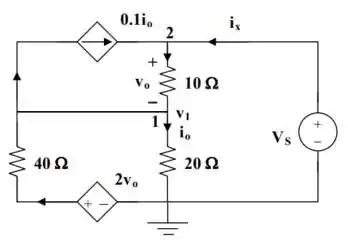
Aplicando a Lei de Kirchhoff da Correntes (LKC) no nó, temos:
Rearranjando:
Passo 3
E, aplicando LKC no nó , obtemos:
Mas note que:
E que:
Dessa forma, a equação referente ao nó fica:
Rearranjando os termos da equação:
Passo 4
Agora, substituindo e e na equação do Passo 2, obtemos:
Resolvendo a equação, podemos encontrar o valor de :
Assim, a resistência de Thevenin é dada por: