Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 4.Problemas - Ex. 88

O resistor variável ( R o ) no circuito da Figura P4.88 é ajustado até que a potência nele dissipada seja 250   W . Determine os valores de R o que satisfaçam essa condição.

Passo 1

Okaaay turminha, bora lá! Começamos encontrando o equivalente de Thévenin em relação a Ro. Depois de fazer algumas transformações de fonte que o circuito simplifica para

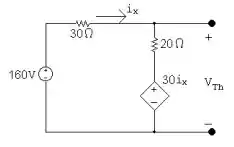
Daí, temos a partir da equação dos nós:

i Δ = 160 - 30 i Δ 50 ;       i Δ = 2 A

V T h = 20 i Δ + 30 i Δ = 50 i Δ = 100   V

Passo 2

Usando o método de fonte de teste para encontrar a resistência de Thevenin, temos:

i T = v T 30 + v T - 30 ( - v T 30 ) 20  

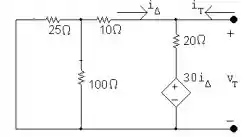
Logo,

i T v T = 1 30 + 1 10 = 4 30 = 2 15

R t h = v T i T = 15 2 = 7.5   Ω

Passo 3

Assim, nosso problema é reduzido a analisar o circuito mostrado abaixo.

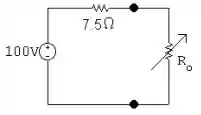
Dessa forma, a potencia do circuito se dá por:

p = 100 7.5 + R o 2 R o = 250

10 4 R o 2 + 15 R o + 56.25 R o = 250

40 R o = R o 2 + 15 R o + 56.25

Resolvendo essa equação, temos:

R o 1 = 22.5   Ω

R o 2 = 2.5   Ω

Logo, essa é a faixa que representa R o .

Resposta

R o 1 = 22.5   Ω

R o 2 = 2.5   Ω

Logo, essa é a faixa que representa R o .

Exercícios de Livros Relacionados

Substitua tudo, exceto o resistor de 4Ω pelo seu circuito equivalente de Thévenin e use o resultado para calcular o i .
Calcule i usando transformações de fontes para obter o circuito equivalente no que se relaciona ao resistor de 1KΩ, contendo uma fonte e um resistor, além do resistor de 1KΩ.
Resolva o Prob 5.17, usando transformações de fontes.
Resolva o Prob 5.16, usando transformações de fontes.
Calcule o equivalente de Thevenin de tudo, exceto o resistor de 4Ω no Prob. 5.16, e use o resultado para encontrar a potência entregue ao resistor de 4Ω .