Enunciado
Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 4.Problemas - Ex. 71
Determine e no circuito mostrado na Figura P4.71 quando for um resistor do Apêndice H tal que .
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!
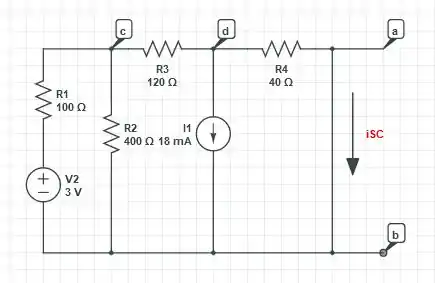
O circuito em questão é dado na figura abaixo. Vamos marcar os terminais dos resistores
como e e obter um equivalente de Thévenin do resto do circuito entre esses terminais.
Para encontrar o equivalente de Thévenin do circuito entre os terminais e , precisamos
para encontrar a tensão de circuito aberto ( ) e a corrente de curto-circuito () entre
terminais e . Então a tensão e a resistência no circuito equivalente de Thevenin estão
E
A tensão de circuito aberto () é marcada como mostrado na figura abaixo. Vamos usar o método de tensão de malha para encontrar .
Indicamos as correntes de malha e no diagrama do circuito conforme indicado no
figura abaixo. A seta curva segue o perímetro da malha e a ponta da seta indica a direção da corrente.
Sabemos que quando uma fonte de corrente é compartilhada entre duas malhas, podemos
combinar essas malhas para formar uma super malha. Indicamos a super malha na figura abaixo figura abaixo. E a equação de restrição da super malha é
Isolando o , temos que
E o circuito equivalente a
Passo 2
Vamos aplicar LKT na malha com a corrente de malha na direção da malha tomando
aumento de tensão como negativo e queda de tensão como positivo, podemos obter
Desenvolvendo a equação, nós temos que
Isolando
Agora escrevemos a equação LKT para super malha tomando o aumento de tensão ao longo da direção da malha como negativa e queda de tensão ao longo da direção da malha como positiva. Então a equação fica
Desenvolvendo
Substituindo por e por , nós temos que
Com isso,
Isolando
Portanto, pode ser obtido como
Substituindo os valores,
Como podemos ver na figura que a corrente através do resistor de é igual para , portanto, usando a lei de Ohm, podemos escrever
Substituindo
Passo 3
A corrente de curto-circuito () é marcada como mostrado na figura abaixo. Uma vez que os terminais e agora estão em curto-circuito, portanto, o resistor de pode apenas ser substituído por um curto-circuito.
Vamos usar o método de tensão de malha para encontrar . Indicamos correntes de malha e e no diagrama de circuito como dado na figura abaixo e a super malha equação de restrição é dada como
Isolando
Com isso, o circuito fica da seguinte forma
Vamos aplicar LKT na malha com corrente de malha na direção da malha tomando aumento de tensão como negativo e queda de tensão como positivo, podemos obter
Agora escrevemos a equação LKT para a super malha tomando o aumento de tensão ao longo da direção da malha como negativa e queda de tensão ao longo da direção da malha como positiva. Então a equação fica
Desenvolvendo,
Simplificando um pouco mais
Substituindo por e por , com isso, nós temos que
Logo
Portanto, pode ser obtida como
Do circuito, podemos perceber que
Então a tensão e a resistência no circuito equivalente de Thévenin são
Substituindo
E a resistência equivalente é igual a
Então, usando este equivalente de Thévenin, a simplificação do circuito em questão é
dado na figura abaixo
Passo 4
Usando o divisor de tensão, nós podemos escrever que
Portanto, usando a Lei de Ohm, a corrente pode ser escrita como
Substituindo os termos, nós temos que