Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 2.Problemas - Ex. 75

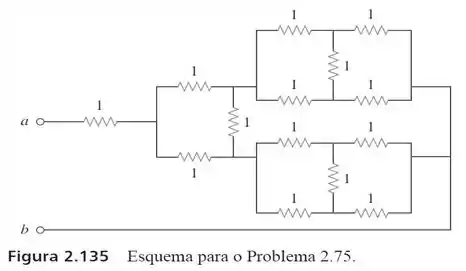
75. Determine R a b no circuito divisor de potência quadridirecional da figura 2.135 . Considere que cada elemento tem resistência igual a 1   Ω .

Passo 1

Bom! A primeira coisa que temos de fazer é destacar algumas partes importantes de nosso circuito! Vamos lá!

Essas partes alaranjadas do nosso circuito tão bem fácil de entender! São configurações triangulares, ou em delta, que não tão muito legal da gente trabalhar. Por isso, vamos fazer a transformação de delta para estrela:

Como todos tem a mesma resistência, vamos fazer o cálculo apenas uma única vez. Pra isso, basta usar as fórmulas já prontas para a conversão de um circuito ∆ em Y . São elas:

R a n = R 2 R 3 R 1 + R 2 +   R 3

R b n = R 1 R 3 R 1 + R 2 +   R 3

R c n = R 1 R 2 R 1 + R 2 +   R 3

Onde:

R 1 = 1   Ω

R 2 = 1   Ω

R 3 = 1   Ω

O que nos leva ao seguinte resultado:

R a n = 1 ⋅ 1 1 + 2 + 1 Ω

R b n = 1 ⋅ 1 1 + 2 + 1 Ω

R c n = 1 ⋅ 1 1 + 2 + 1 Ω

R a n = 1 3   Ω

R b n = 1 3   Ω

R c n = 1 3   Ω

Passo 2

E com isso, chegamos ao seguinte circuito:

Nós queremos descobrir o valor da resistência equivalente R e q ao longo de a - b . Ora bolas! Tá na cara que ela é dada por:

R e q = 1   Ω + 1 3 Ω + 1 3 Ω + 1 Ω | | 1 3 Ω + 1 Ω + 2 3 Ω | | 1 3 Ω + 1 Ω | | 1 3 Ω + 1 Ω + 2 3 Ω    

R e q = 1   Ω + 1 3 Ω + 4 3 Ω | | 4 3 Ω + 2 3 Ω | | 4 3 Ω | | 4 3 Ω + 2 3 Ω

R e q = 1   Ω + 1 3 Ω + 4 3 Ω ⋅ 4 3 Ω 4 3 Ω + 4 3 Ω + 2 3 Ω | | 4 3 Ω ⋅ 4 3 Ω 4 3 Ω + 4 3 Ω + 2 3 Ω

R e q = 1   Ω + 1 3 Ω + 2 3 Ω + 2 3 Ω | | 2 3 Ω + 2 3 Ω

R e q = 1   Ω + 1 3 Ω + 4 3 Ω | | 4 3 Ω

R e q = 1   Ω + 1 3 Ω + 4 3 Ω ⋅ 4 3 Ω 4 3 Ω + 4 3 Ω

R e q = 1   Ω + 1 3 Ω + 2 3 Ω

R e q = 1   Ω + 1   Ω

R e q = 2   Ω

Resposta

R e q = 2   Ω

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule (a) a resistência equivalente vista pela fonte, (b) a corrente i , (c) a potência entregue pela fonte, (d) v 1 , (e) v 2 e (f) 0 valor nominal mínimo (wattagem) necessário para 0 resistor de 4
Se i 1 = 9 e i 2 = 6 na Fig. 2.17 (a) calcule a relação R 2 // R 1 .
Calcule a resistência equivalente, vista pela fonte, e use este resultado para encontrar i ,i 1ev .
Na Fig. 2.18, se N = 3, R 1 = 9 Ω ,R 2 = 72 Ω , e v = 12 s e ntV e o valor da potência instantânea entregue pela fonte de corrente é 24 s e n 2 tW , calcule (a) R 3 , (b) i e (c) i 3
Calcule a resistência equivalente vista pela fonte e a corrente i .