Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 3.Problemas - Ex. 48
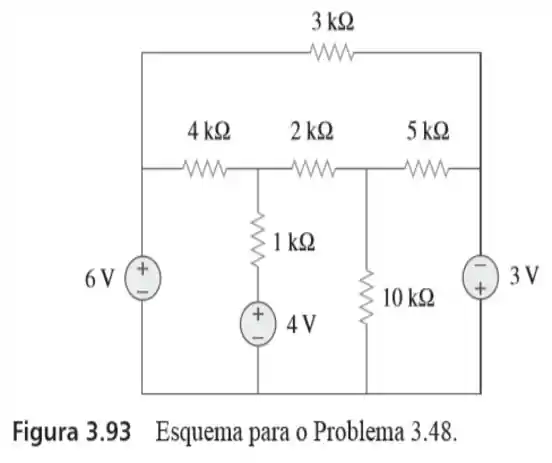
48. Determine a corrente que passa pelo resistor de no circuito da figura , usando análise de malhas.
Passo 1
Bom! Se estamos trabalhando com análise de malhas, então temos que nomear as correntes de malha de cada uma das quatro malhas do nosso circuito. Ah!
Bora fazer então, o esboço das corrente de malha que nele estão presentes...
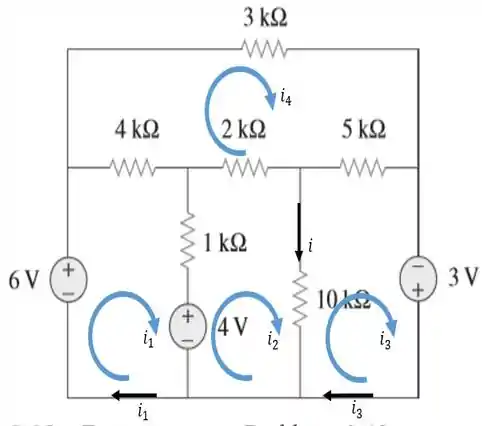
E agora, vamos aplicar a análise de malhas pra esse nosso circuito.
Bora primeiro percorrer a malha . Olha só! O objetivo aqui, é determinar as tensões nessa malha. E para isso, consideremos as quedas de tensão como positivo e as elevações de tensão como negativo. A soma disso tudo tem que dar zero...
Passo 2
Em seguida, bora percorrer a malha . Repetindo o mesmo procedimento do , obtemos a seguinte relação:
Passo 3
E depois, a malha :
Passo 4
E por fim, a malha :
Passo 5
Obtemos assim, o seguinte sistema de equações:
Bom! A questão pede pra gente resolver esse problema com o uso do . Mas como não temos , vamos apelar pro mesmo, que é bastante parecido. Afinal, praticidade é tudo que a gente quer, né não?
Olhas só! Esse sistema de quatro equações e quatro incógnitas pode ser escrito na forma matricial, como:
Ou seja, o sistema pode ser escrito em função de três matrizes. Vamos dar nomes a elas...
Sabe uma coisa legal de trabalhar com sistemas lineares em matrizes. Para obter a solução desse sistema linear, basta usar a seguinte relação:
Passo 6
Agora, vamos fazer isso como no . A matriz vai ser escrita assim, nesse software...
E a matriz fica desse jeito...
Fazendo , podemos obter nossa resposta...
Desse jeitinho aqui:
Por fim! A questão nos pede para obter o valor da corrente que circula no resistor de .
Ora bolas! Pela figura do , podemos ver que:
E voilà! Encontramos nossa resposta!