Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 2.4 - Ex. 5
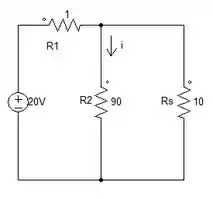
Calcule a resistência equivalente vista pela fonte e a corrente
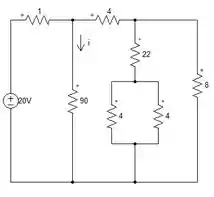
Passo 1
Essa questão pede o e a corrente , a qual está passando no resistor de 90 Preste atenção para esse circuito. Teremos que fazer associação em paralelo e em série!
Lembrando que, associação em paralelo fazemos: Ex:
Associação em série basta somar.
Primeiro vamos fazer o resistor de 4 em paralelo com o de 4
Esse resistor de está em série com o de
Esse resistor de 24 em paralelo com o de 8.
Esse resistor de está em série com o de
Esse resistor de 10 em paralelo com o de 90.
Esse resistor de está em série com o de
Passo 2
Show de bola! Já temos o nosso , agora vamos saber o valor da corrente . Mas antes vamos descobrir o . Para isso, vamos fazer lei de Ohm.
Depois de termos descobertos a corrente equivalente, vamos ter que fazer divisor de tensão por estarem em uma associação em paralelo,
